チェバの定理・メネラウスの定理 チェバの定理・メネラウスの定理 三角形ABCの辺BC,CA,AB上に点D,E,Fをとり、線分AD,BE,CFが1点Gで交わるとき、以下の等式が成り立つ。 チェバの定理の証明 図のように、a= BCG、b= CAG、c= ABGとします。 AF/BF=b/a、BD/CD=c/b、CE/AE=a/c より、 (AF/BF)(BD/CD)(CE/AE)=(b/a)(c/b)(a/c)=1 メネラウスの定理の証明ブリタニカ国際大百科事典 小項目事典 力の三角形の用語解説しかも 個以上の三角形を見つけられれば、IQ1以上確実! ということで、この問題は多くのTwitter民たちのクイズ心に火を点けたもよう。ネット上には様々な回答が寄せられている。 あなたはいくつの三角形が隠れているか分かるだろうか?
Documen Site Download Sanheihou Theorem Pdf
ディスプレイ 三角形 の 法則
ディスプレイ 三角形 の 法則-三四五(さしご)とは 古くから建築の世界で使われてきた 「矩(かね)」を出すための手段です。 建築の世界では直角の事を「矩(かね)」あるいは「矩手(かねて)」と言います。 建築現場で 丁張り(ちょうはり) などの墨出しの際に使われてき人際關係的終極法則! 絕對有效! 3秒鐘瞬間提升「人際關係」! |ARC三角形|張邁可 If playback doesn't begin shortly, try restarting your device




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
三角形の外心、三角形の外接円 この1点で交わった点 o を三角形の外心という。 外心 o を中心として、半径 oa の円が三角形 abc の外接円である。 oa=ob=oc ol⊥bc 、 om⊥ac 、 on⊥abS formula (1) area S = √s(s−a)(s−b)(s−c) s= (abc) 2 T r i a n g l e b y H e r o n ′ s f o r m u l a ( 1) a r e a S = s ( s − a) ( s − b) ( s − c) s = ( a b c) 2 お客様の声 アンケート投稿 よくある質問天体の位置計算では球面三角形の問題を解く場面があります。ここでは球面三角形の基礎的な法則を理解します。 球面三角形の正弦法則 平面obcを基準面とし、aからこの基準面に垂線aa'をおろす。 a'からobとocに垂線a'b'とa'c'をひく。
あなたはどんな法則を知っていますか? 今日は私が大切にしている 人生の三角形の法則について お伝えしていきます! この法則は、さまざな場面で 当てはめることができるので 知っておいて損はしない法則です☆ 人生の三角形の法則とはデジタル大辞泉 正弦定理の用語解説 三角形の角と辺の関係を示す定理。平面上の三角形の頂点をA・B・C、対する辺をa・b・cとするとき、a/sinA=b/sinB=c/sinC=2R(Rは外接円の半径)が成り立つというもの。正弦法則。三角形定则 是平面力系求解力的合成与分解的基本法则 1 有两个成α(0
法則の辞典 象限の法則(球面三角法)の用語解説 (1) 直角球面三角形において,直角以外の角とその対辺は同じ象限にある.(2) 直角球面三角形において,2辺が同じ象限にあれば,残りの辺は第一象限にある.もし2辺が異なる象限にあれば,残りの辺は第二象限にある.お互いの違いを乗り越えたコミュニケーションになるのか トレーニングしていきます。 タヨナの法則 その1 「三角形を整える」 タヨナの法則 その2 「三角形をコントロールする (大きさ・スピード)」 タヨナの法則 その3 「三角形で進む方向を変えるTap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations




三角形の成立条件とその証明 高校数学の美しい物語




人生には三角形の法則がある カラダとココロが繋がる 自分に還る 内観アドバイザー Yuiのblog
類似した形・色・パターンから、重なり合っていたとしても違いを認識し、区別することができる。 「単純性の法則(Law of Simplicity)」とも言われる。 以下の①は、②のように3つの円が重なったものとして認識され、③の形の集合体と認識されることはない。 ってことは、この三角形は3 4 5の直角三角形ってことがわかるね。 bc ab = 3 5 になってるはずだから、 abはbcの3分の5倍だね。 よって、 ab = bc× (3分の5) = 10 cm になるね。 3 4 5の直角三角形の比もよく出てくるからしっかり押さえておいてね。直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°,60°,90°の 直角三角形 45°,45°,90°の 直角三角形 3辺の比は となります。 3辺の比は




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角形の法則なら1分でディスプレイが完成する インテリアコーディネーター荒井詩万のブログ
って聴いたことありますか? 私は、その法則の存在を知ってはいましたが、それを論理的に説明されたのは初めてでした!! ↓↓↓ 恋愛三角形の法則とは 直角三角形を イメージしてください。 左下の角が自分 左上が進化した自分 右下が運命のお愛手 とします。初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem)は、直角三角形の3辺の長さの関係を表す。斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は c 2 = a 2 b 2 {\displaystyle c^{2}=a^{2}b^{2}} が成り立つという等式の形で述べられる。三平方の定理(さんへいほうのていり)、勾股弦の定理(こうこげんのていり)とも呼ばれる。 ピタゴラス今回は二つの方法で第2法則を導いてみます。 面積速度の保存その1 惑星の軌道が楕円の時、面積速度は V s = 1 2r2˙θ (3) (3) V s = 1 2 r 2 θ ˙ で表される。 そして、万有引力の下ではこの量は保存する。 即ち dV s dt = 0 (4) (4) d V s d t = 0 導出方法の一つ目です




三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ




世界に一つだけの 三角形ペア 発見 慶大院生2人証明 朝日新聞デジタル
タレスの定理 (タレスのていり、 英 Thales' theorem )とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理 、 タレースの定理 ともいう。まず、球面上の直角三角形を考える。 OB BD = 1 BD =BD・・・② OB BE = 1 BE =BE・・・③ ①、②、③より sinA= c a sin sin となる。 平面三角形の場合の正弦(サイン)は次のようであった。 (高等学校数学Ⅰ、啓林館、1997) C= 2 π (=直角) とする。 A B C ABC ABC A D E ADE ADE = A B ⋅ A C ⋅ sin ∠ A A D ⋅ A E ⋅ sin ∠ A = A B ⋅ A C A D ⋅ A E =AB\cdot AC\cdot \sin\angle AAD\cdot AE\cdot \sin\angle A\\=AB\cdot ACAD\cdot AE = AB ⋅ AC ⋅ sin∠A AD ⋅AE ⋅sin∠A = AB ⋅ AC AD ⋅ AE 「角を共有する三角形の面積比は線分の積の比に変換できる」 と覚えておきましょう。 この公式の頻出応用例として,




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



2
三角形の内角の性質 三角形の内側にある角のことを 内角 といい、 すべて足すと180° になります。 これは小学生のときに学習しているので覚えている方も多いでしょう。 でも じゃぁ、何で180°になるのか知っていますか? と言ったら、困ってしまい法則その(1)三角形にまとめる 背の高いもの1つと低いもの1~3つをそれぞれ決めます。 背の高いものを三角形の頂点にして、低いものをとの間をゆるやかに埋めるように他の雑貨を飾っていきます。 奥行きの無い場所では頂点から左右に並べる飾り方を 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学



パスカルの三角形と最短経路 思考力を鍛える数学
ハインリッヒの災害三角形 横線で区切られた三角形で図示されることから「ハインリッヒの(災害)三角形/ピラミッド」(Heinrich's triangle/pyram id)」等と呼ばれるもので、「ハインリッヒの法則」といえばこのハインリッヒの三角形を指すことが多い。逆三角形型の文章を書くには 三角形型は物語調ですから,それでどうなるのだろうと思いながら読み進めてもらうにはよい のですが,手っ取り早く何が書いてあるのかを伝えるという点では適しているとは言えません。 それに対し,逆三角形型は何が書い 逆三角形の法則 そう、お客さんにプレゼンするには この順番、法則がすごく大事です。 今日の話は、会社のコンセプトを 決めるのと同じくらい 重要な内容ですので、 ぜひ時間を作って考えてみてくださいね。 それでは今日は この辺で失礼致します。



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
"三角形の法則なら1分でディスプレイが完成する" 著書『今あるもので「あか抜けた」部屋になる。』 お部屋づくりののルールを紹介していまして、その中の1つです。 先日出演したnhk 「あさイチ」でもお話しました。 この赤い三角形はスタッフさんの三角形の証明・形状問題 → 携帯版は別頁 → 印刷用PDF版は別頁 三角関数の加法定理,倍角公式,3倍角公式,半角公式 三角関数の和や積には多くの公式がありますが,「 加法定理は覚える,他は作る」 というのが,作者おすすめの考え方ですS = s ( s − a ) ( s − b ) ( s − c ) {\displaystyle S= {\sqrt {s (sa) (sb) (sc)}}} ただし s = a b c 2 {\displaystyle s= {\frac {abc} {2}}} また、以下のような s を用いない表記もある。 S = ( a b c ) ( − a b c ) ( a − b c ) ( a b − c ) 4 {\displaystyle S= {\frac {\sqrt {




ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ




逆三角形の法則でロジックを絞り込みましょう 地方自治体の宣伝や広報でお悩みの担当者さん 必見 宣伝の新しい形
ハインリッヒの法則 (ハインリッヒのほうそく、Heinrich's law)は、 労働災害 における経験則の一つである。 1つの重大事故の背後には29の軽微な事故があり、その背景には300の異常(ヒヤリ・ハット)が存在するというもの。 「 ハインリッヒの災害トライアングル定理 」または「 傷害四角錐 」とも呼ばれる。この三角形に並べられた数字には、次のような法則があるのがわかります。 「ある数は、その1つ上の行の隣接する左右の数の和によって求まる」 例えば、上図の赤い部分では、 6+4=10 となっていま余弦定理(よげんていり、英 law of cosines, cosine formula)とは、平面上の三角法において三角形の辺の長さと内角の余弦の間に成り立つ関係を与える定理である。余弦定理を証明するために用いられる補題はときに第一余弦定理と呼ばれ、このとき証明される定理は第二余弦定理と呼ばれ区別されることがある。単に余弦定理と言った場合、第二定理を指す。 三角形の角



三角形の2辺の和と差




直角三角形の辺を求める Youtube




三角形の重心の性質とその証明 求め方 数学a By となりがトトロ マナペディア



1
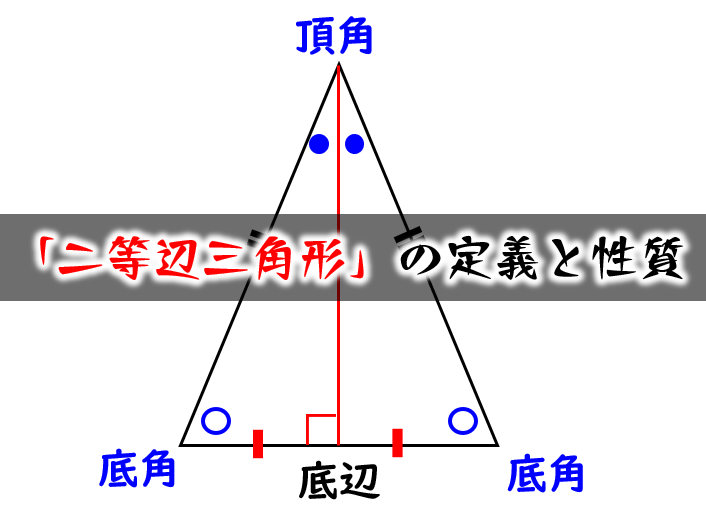



二等辺三角形の定義と性質 問題の解き方 数学fun




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名




Diy上達法 サシゴの法則とは クリエイティブライフ アトリエ1625




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube



七五三 三角形から円に内接する四角形へ



1




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー
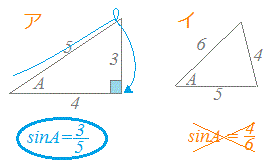



正弦定理



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs
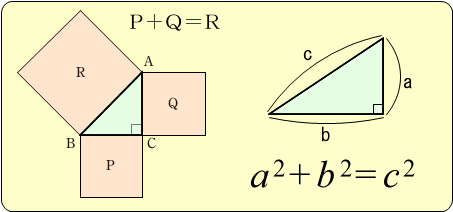



見えますか タイルの模様からピタゴラスの定理 Note Board




三角比 30 45 60 もう一度やり直しの算数 数学




余弦定理で角度を求める方法 数学の星




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




三平方の定理で辺を求める Youtube




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



図形の扉 三角形の外角の定理




直角三角形 Wikipedia




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
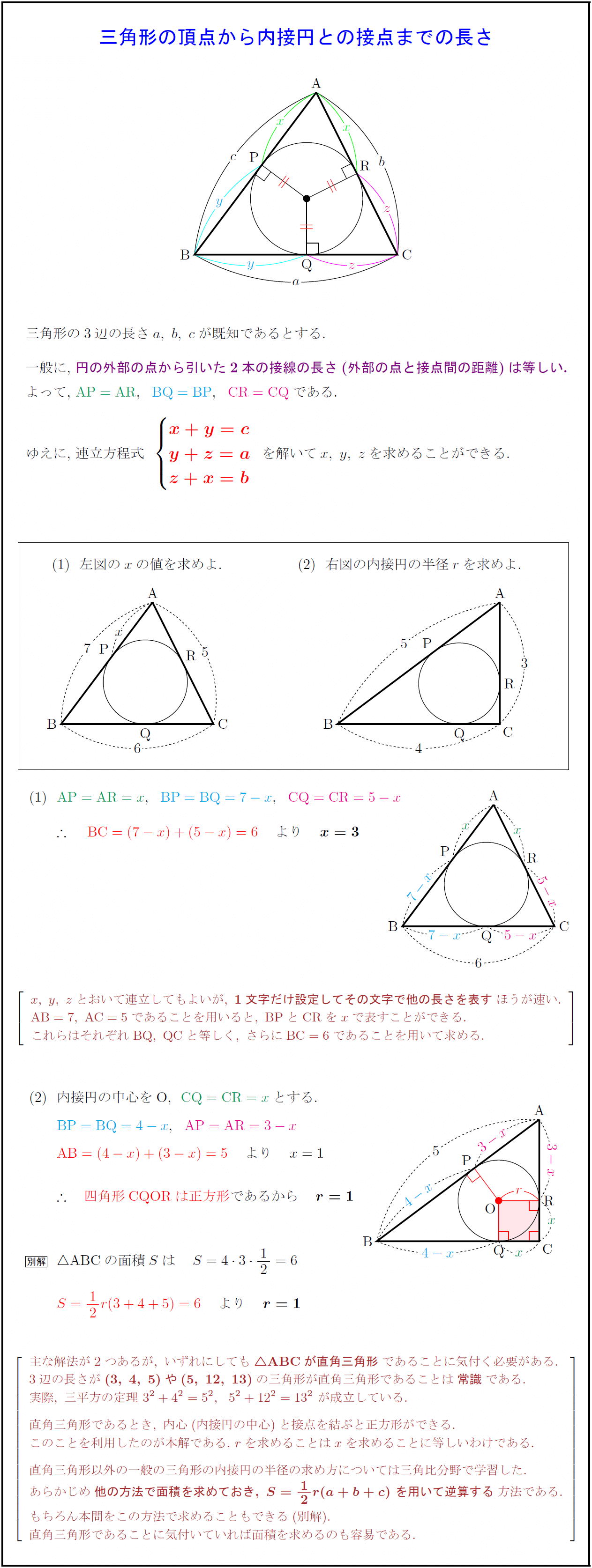



高校数学a 三角形の頂点から内接円との接点までの長さ 受験の月



1



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



Documen Site Download Sanheihou Theorem Pdf




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




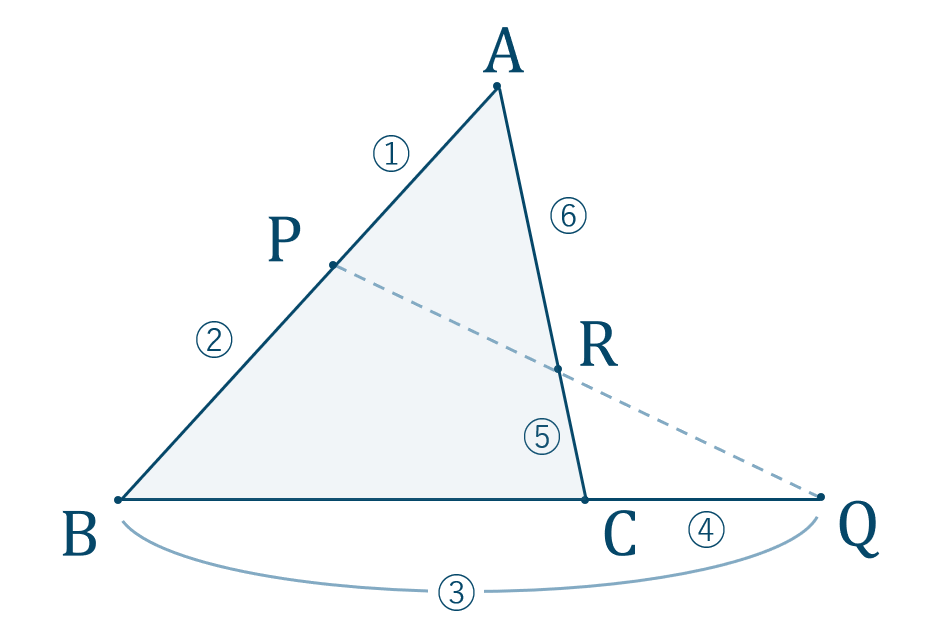
メネラウスの定理が5分でわかる 証明や使い方をイラスト入りで詳しく解説



数学のコツ 三平方の定理 個別指導ソラオトのスタッフブログ



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める



パスカルの三角形と最短経路 思考力を鍛える数学



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
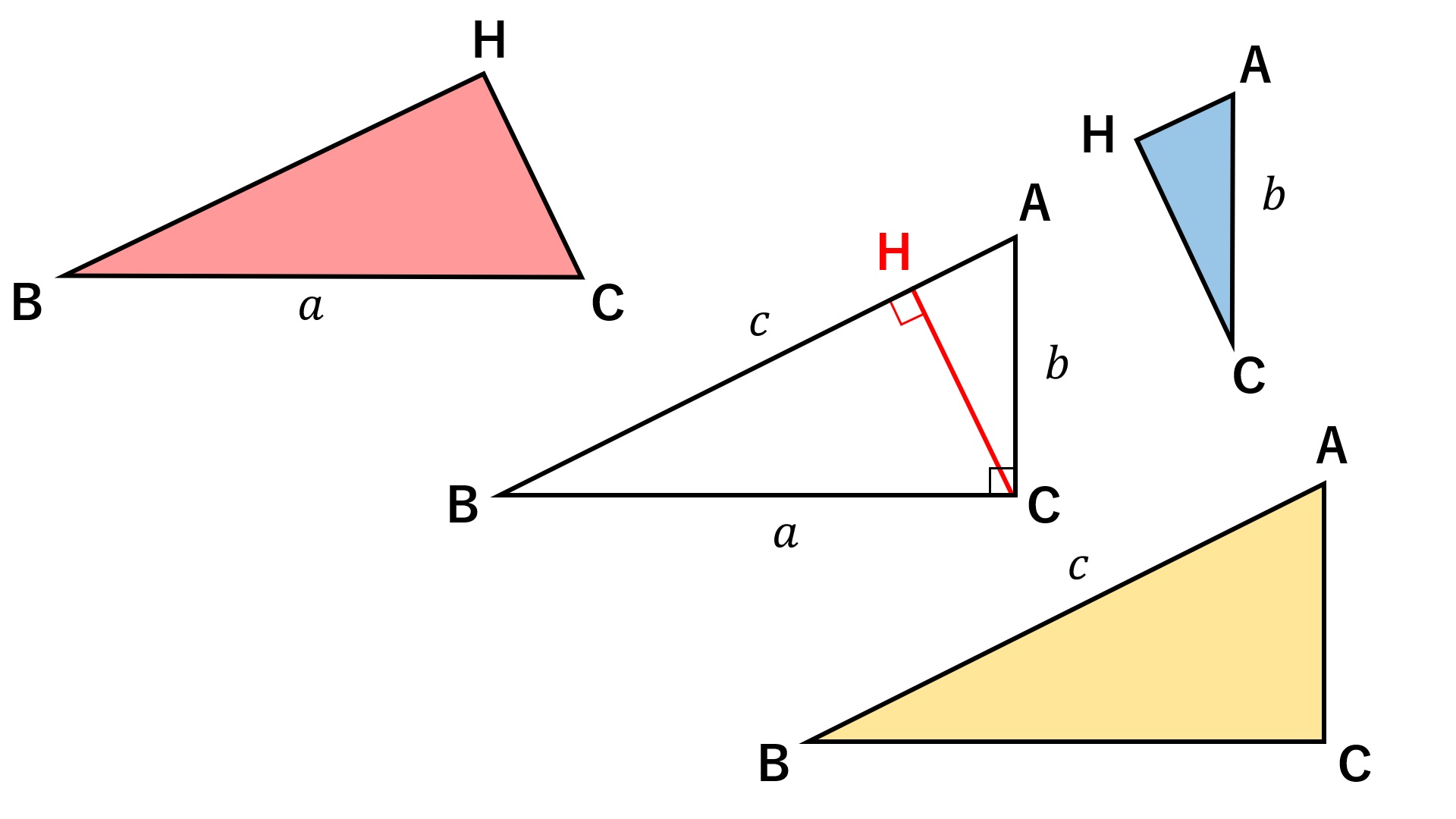



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ



3




直角三角形の辺の長さ 合同条件 面積について アタリマエ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
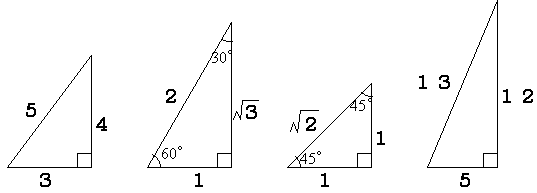



三角形の性質
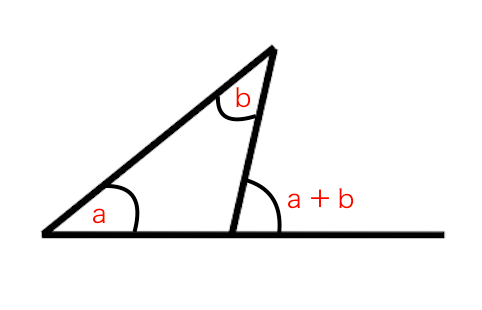



外角の定理とは 苦手な数学を簡単に




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su



Newみんなの算数講座86 三角形を全部見てはいけない 中学受験の算数知恵宝庫




逆三角形の法則 Or The Rules Of The Inverted Triangle General Discussions Cardano Forum




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




三平方の定理と二等辺三角形 Youtube



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ The 2nd
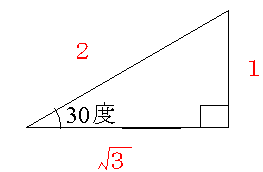



三角形の性質
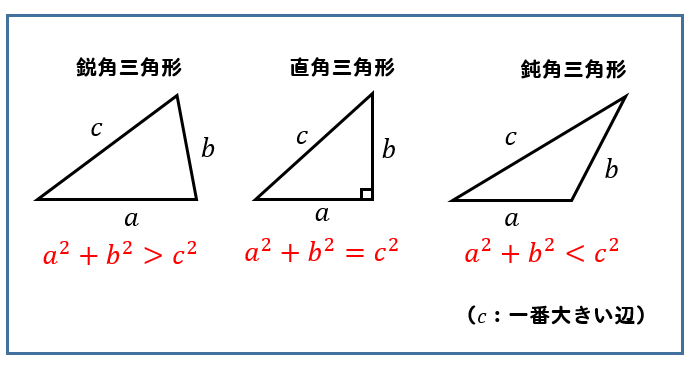



鋭角 鈍角三角形 三平方の定理を使って見分ける方法を解説 数スタ




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学
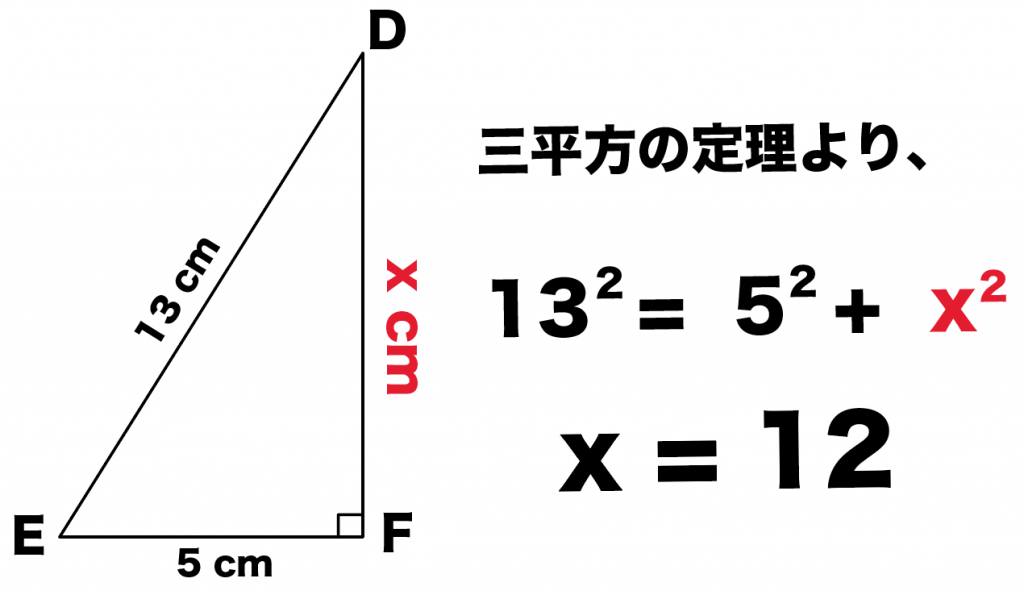



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
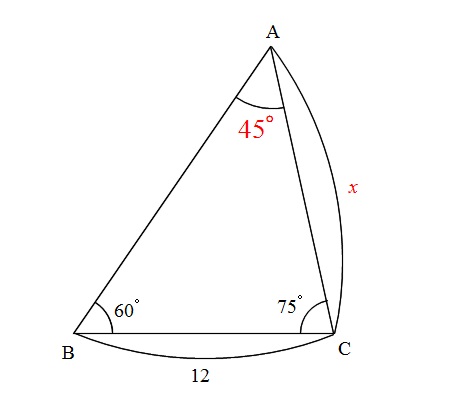



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない




パスカルの三角形と二項定理による展開との関係とは 二項係数の性質を証明 遊ぶ数学



三角形の性質



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
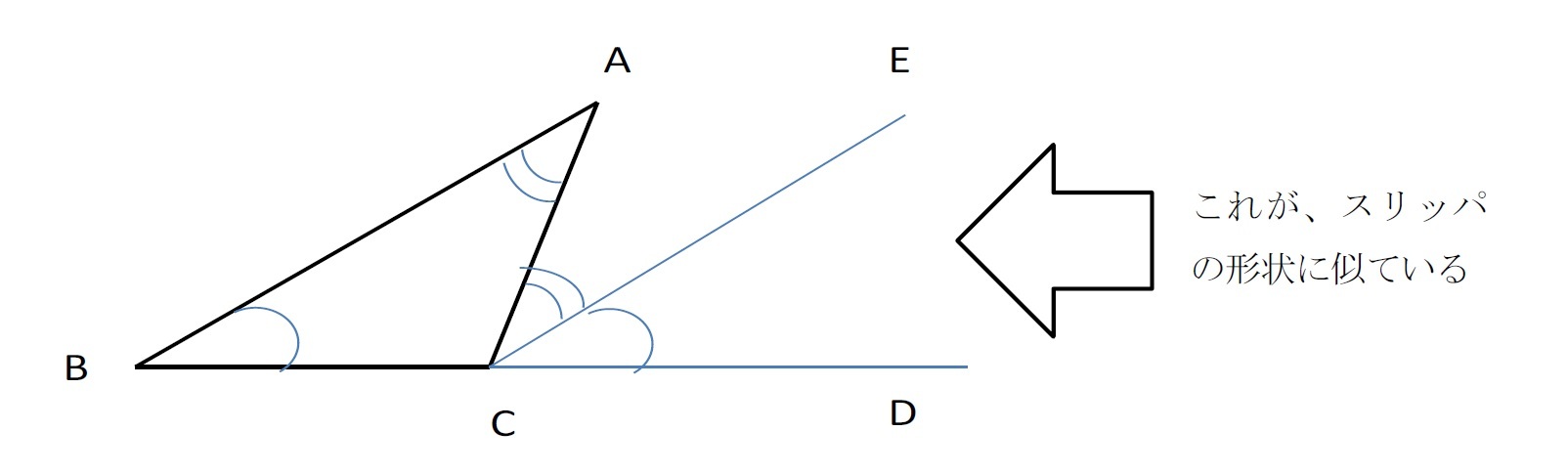



スリッパの法則 って 知っていますか ニッセイ基礎研究所




iq問題 三角形の中にある法則で数字が並んでいます 法則がなりたつとしたら にはなにがくるのか Jyankquiz




鏡の法則の本質的な意味 鏡の法則は実は三角形だった 一家に一人のセラピストー戦場で働く男性を癒すパートナーシップ論ー ライフシフト総合研究所



七五三 三角形から円に内接する四角形へ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
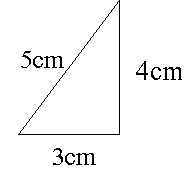



三角形の性質
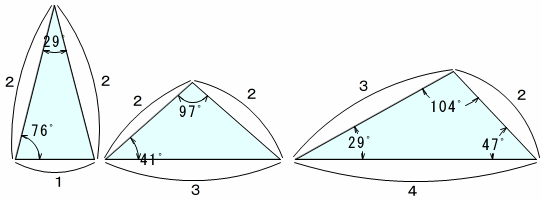



3 4 5の三角形で 本当に直角ができる Note Board
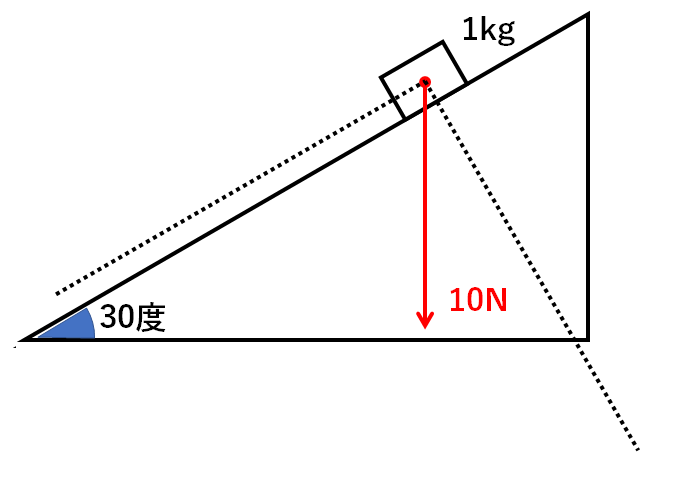



中3物理 分力と三平方の定理 中学理科 ポイントまとめと整理




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
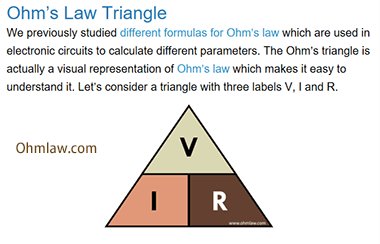



Kistenkasten723 オームの三角形 日本では オームの法則の図は 円で描かれるが 英語圏やドイツ語圏では 三角形で表現され Ohm S Law Triangle と呼ばれる 掛算 超算数 算数 算数教育 オームの法則 みはじ図 くもわ図 きはじ T Co




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座
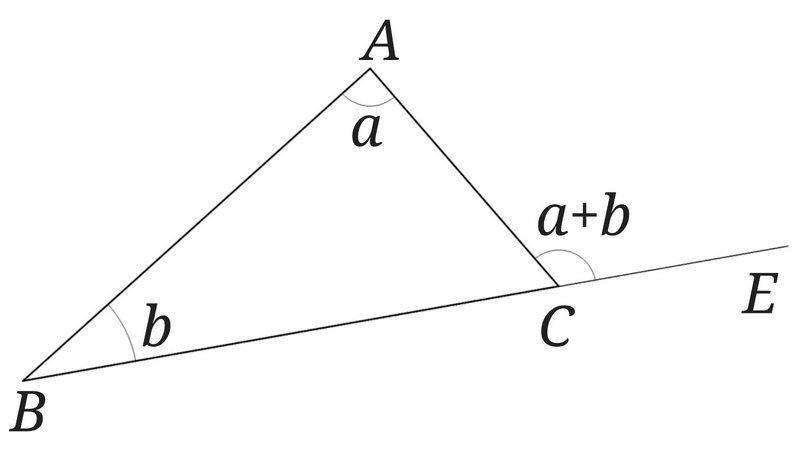



数学の図形で使えるスリッパの法則を使って星の角度の和をだそう まぜこぜ情報局




三角比 三角関数の定義 相互法則や90 8の関係など 数学の偏差値を上げて合格を目指す



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学受験算数 等積変形の利用 ヒポクラテスの月




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
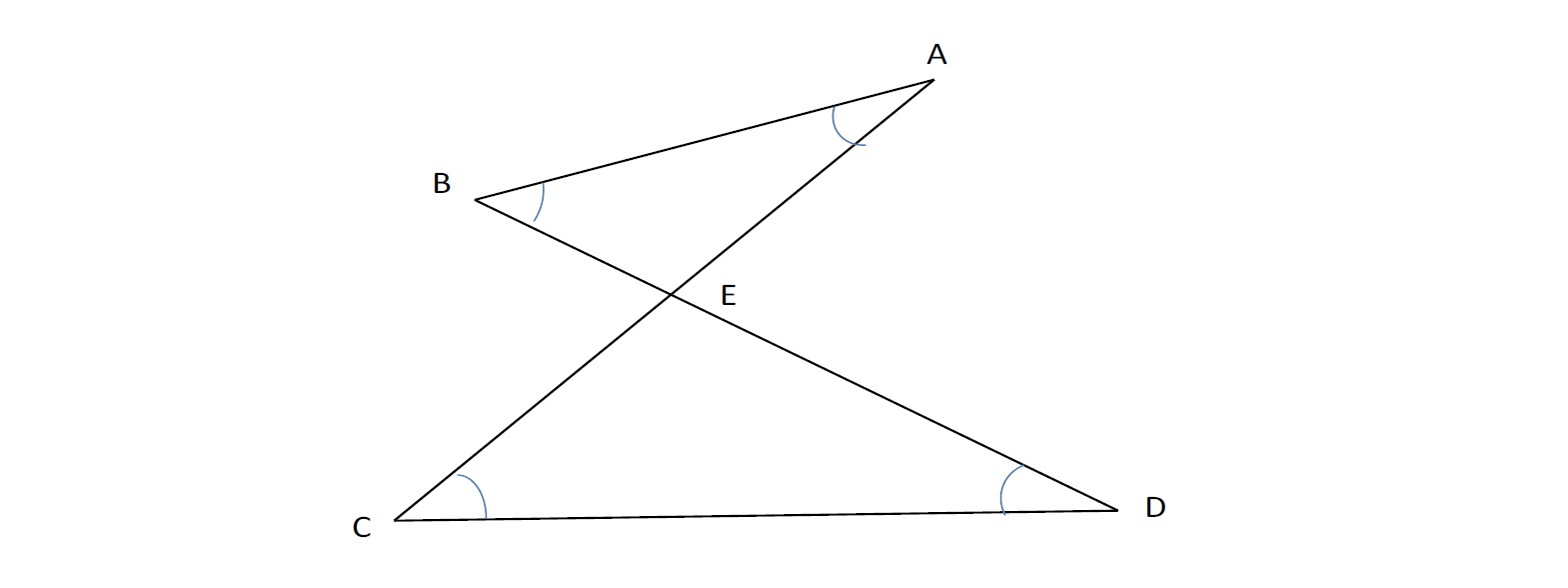



スリッパの法則 って 知っていますか ニッセイ基礎研究所




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



三平方の定理




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三角形の決定条件と自由度 高校数学の美しい物語



0 件のコメント:
コメントを投稿