《三角形の面積の求め方》 三角形の面積=底辺×高さ÷2であることから 答え 28㎠ 問題③ 次の三角形の面積を求めましょう。 《三角形の面積の求め方》 問題①・②と比べると三角形の形が傾いていますが、この三角形の面積を求める際に使う底辺は10cm。正三角柱の体積と底辺から高さを計算します。 正四角柱の底辺と高さから体積と表面積を計算します。 正四角柱の体積と底辺から高さを計算します。 正六角柱の底辺と高さから体積と表面積を計算します。 正六角柱の体積と底辺から高さを計算します。 正四角錐の底辺と高さから体積、側面積、表面積を計算します。 正四角錐の側辺と底辺から高さ、体積、表三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は,四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形,側面が1辺の長さ4cmの正三角形です。

โน ตของ 体積 表面積 側面積 の公式 ช น Junior Clear
三角形の体積の求め方 公式
三角形の体積の求め方 公式-公式というより考え方が重要。 正三角形の面積,正四面体の体積 正三角形の面積はもちろん,正四面体の体積も一瞬で求められるようにしておきましょう。 サラスの公式 座標平面,座標空間上での求積はサラスが強力。 ベクトルの定番問題の公式(面積比)数学・算数 三角形の面積の公式について 中学数学を教えていらっしゃる方、もしくは詳しい方、教えてください。マニアックな質問です。 小学校で習う、三角形の面積の求め方、 底辺×高さ÷2 は、中 質問No




立体の体積を求める公式
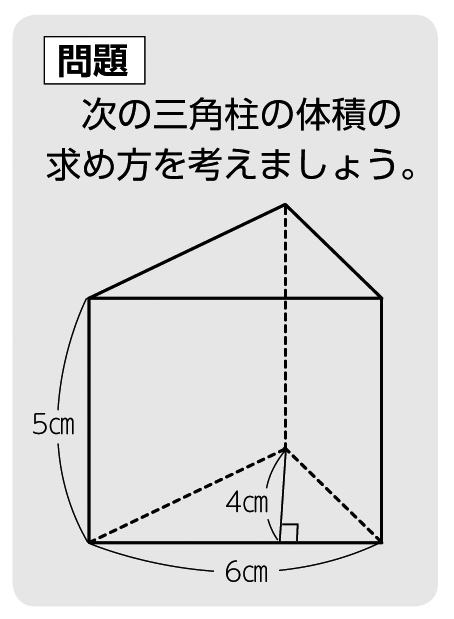
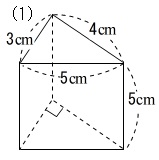
切断三角柱の体積の求め方 三角柱の両端が切断された切断三角柱の体積を求めるときは、上記の操作を2回繰り返すことで求めることができます。 三角形に内接する正方形の作図法の補足二等辺三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と底角 斜辺と高さ 斜辺と底角 高さと底角 面積と底辺 面積と高さ 面積と斜辺 面積と底角 高さ底面の形は直 角 三 角 形 な 三角柱の体積は,角柱の体積の公式を使って求めることができる。 ので,三角形の面 積 の 公 式 を 底面の形が直角三角形なので,三角形の面積の公式を使って底面積を求めると, 4×3÷2と表すことができる。
三角錐の体積 三角錐は、底面が三角形で上面が尖っている形状です。三角錐の体積は、三角柱の体積を1/3にすればよいです。三角形の底辺が3、高さ4、三角錐の高さが5のとき 三角錐の体積=3×4÷2×5÷3=10cm 3 です。 まとめ○三角錐,四角錐,円錐の体積 V は,それがちょうど入る四角柱,三角柱,円柱の体積の です. ○特に,円錐については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから 三平方の定理直角三角形の辺の長さを計算する4つの問題の解き方 中2数学 簡単公式平行四辺形の面積の求め方がわかる3ステップ 中2数学 簡単公式長方形の面積の求め方がわかる3ステップ 中2数学
方 1 三角柱の体積を計算で求める方法を 理解する。 既習の立体の体積の求め方を手がかりに、角 柱の体積の求め方を見直す。 *底面が直角三角形の三角柱の体積も、底面積 ×高さで求められることを考える。 2 一般の角柱の体積の公式をまとめ る。『円錐の体積が円柱の1/3なのはなぜなの?』 1、三角形と錐体を比べる t:こういう時は、よく知っているものと比べながら考えるとわかるよ。錐体は何かと似ていない? s:三角形だ。 t:そうだね。「三角形と四角形」は「錐体と柱」に似ている。三角柱の体積を求める 1 公式を用意する 公式は V(体積) = 1/2 x l(長さ) x w(幅) x h(高さ) となります 。 V = 底面の面積 x 高さ が基本となっています。




体積の求め方 計算公式一覧




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
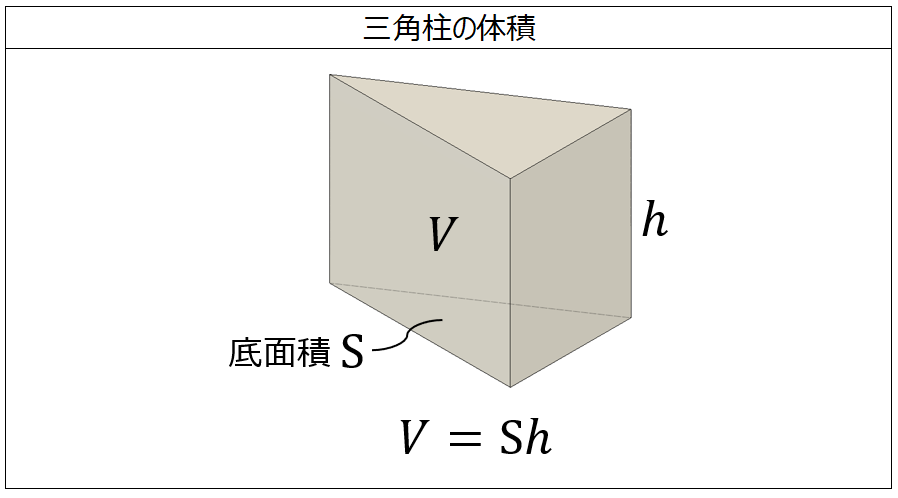
三角形の3辺が与えられたときの面積の求め方 「3辺の長さが,5,4,7の三角形の面積を求めよ。」という問題がわかりません。面積を求めるときは,公式 S=1/2bc sinA に当てはめればいいことは三角柱や四角柱などの体積は、底面積 $S$、高さ $h$ として、次の式で求められます。 角柱 ( かくちゅう ) の体積 \begin{align*} V = Sh \end{align*}三角柱の体積・表面積の求め方をマスターしよう! 作図円に内接する正三角形の作図方法とは? 平面・空間図形 作図三角形の高さをコンパスを使ってかく問題を解説!



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
三角形の辺の長さによるからです。 まとめ 今回は三角柱の体積の公式、計算について説明しました。三角錐の体積の求め方 三角錐oabcについて、 OA=OB=OC=5 AB=4 BC=5 AC=6 この三角錐の体積の求め方を教えていただけませんか? 三角柱の高さ=三角柱の体積÷底面積 で求めることが出来ます。 ここで底面積=8×5÷2=(㎠) よって求める三角柱の高さ=180÷=9(cm)となります。 答え 9cm 三角比を用いた三角形の面積の求め方 三角形の面積の求め方といえば、小学校で習う、 $$\text{底辺} \times \text{高さ} \div 2 = \frac{1}{2} \times \text{底辺} \times \text{高さ}$$ が有名ですよね。 実は三角比を利用することで三角形の面積を求められます。




多くの教師が失敗する角柱の体積の求め方 算数を究める




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト
三角錐,四角錐,円錐,の錐 (すい)という漢字は訓読みでは「きり」と読みます.これは,小さな穴を開けるための先のとがった工具です. 三角錐や円錐といった「錐」とは,穴をあける道具のように先の尖った立体です. では,「〇〇錐」の体積の求め方はどうだったかというと, (〇〇錐の体積) = (底面積)× (高さ)× 1 3 ( 〇〇錐の体積) = ( 底面積) × ( 高さ) × 1台形の底辺と計算(求め方)、上辺の関係 台形の底辺は、 高さ 面積 上底(または下底) が既知のとき計算できます。 三角柱、角錐の体積の求め方は下記が参考になります。この円柱において, 底面の面積は,π×22=4π(cm2), 高さは 2cm なので, 円柱の体積=底面の面積×高さ より, 体積は,4π×2=8π(cm3)となります。



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術



計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく
や平行四辺形にして、三角形の面積 の求め方を考えることができる。 右の図の平行四辺形の面積 を求めましょう。 三角形の面積の求め方を考えよう。 ・長方形に変形して求める。 ・2倍にして長方形や平行四辺形にして、その 半分が三角形の面積になる。 そして、長方形は、 元々同じ直角三角形を二つ合わせたもの だったので、 最初の直角三角形の面積の2倍 となっています。 よって、元々の直角三角形の面積は、長方形の面積の × 1 2 (= ÷ 2) であるから、 24 ÷ 2 = 12小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



地図の体積計測
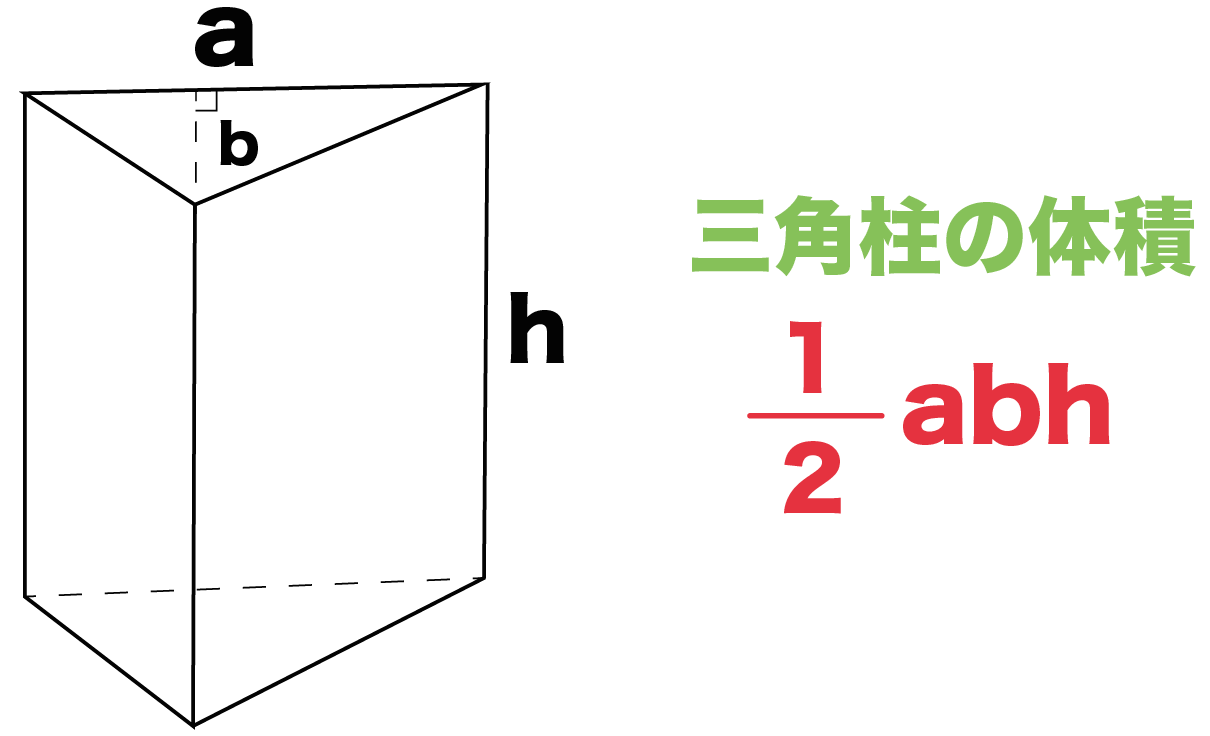
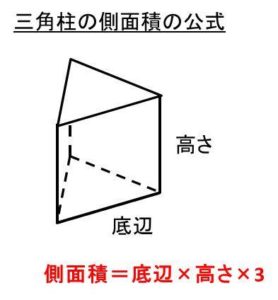
三角柱(さんかくちゅう)の体積は下記の公式で求めます。 三角柱の体積=(底辺×高さ÷2)×三角柱の高さ 下図をみてください。これが三角柱です。底面が三角形、側面が四角形からなる立体図形です。 三角形の底辺をb、高さをa、三角柱の高さをhとします。平行四辺形,三角形などの面積の求め方を理解する。知 6 本時の授業 (1)題材名 三角形の面積の求め方 (2)ねらい 三角形の面積の求め方を理解する。 既習の図形の面積の求め方と関連付けて,三角形の面積をいろいろな方法で求めようとし関 ている。三角形の求め方をしっかり覚えて、スムーズに求められるまで繰り返し学習しましょう。 1辺と2つの角が与えられたとき 例えば,図のように,bとA,Bの大きさが与えられた場合にも,与えられた条件をもとに, の公式が使えるようにします。



1



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生
正多角形をすべての対角線で分けた二等辺三角形の面積を求めて、その和を求める方法もあるので、上記の公式を無理して覚える必要はありません。 (二等辺三角形に分ける方法については、計算問題①で解説します!) 正 n 角形の面積の公式(n = 3, 4, 5, 6)「底辺 a の正三角形」の高さは h = a 2 − (a / 2) 2 = 3 2 a ③ 2辺とその間の角の大きさを使った公式 2辺の長さ a, b とその間の角 θ が分かっている場合、その三角形の面積は 三角形の面積 三 角 形 の 面 積 S = 1 2 a b sin・正三角形(面積から辺と高さ) 正三角形の面積から1辺の長さと高さを計算します。 直角三角形 ・直角三角形(底辺と高さ) 直角三角形の底辺と高さから、斜辺と角度と面積を計算します。



1



三角錐とは 体積 表面積の公式や求め方 受験辞典
三角柱の体積は底面積を求めて、高さを掛けるだけで完成です! 底面である三角形の面積が、\((底辺)\times(高さ)\times \frac{1}{2}\) で求めれるので次のような計算になります。




多くの教師が失敗する角柱の体積の求め方 算数を究める




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ
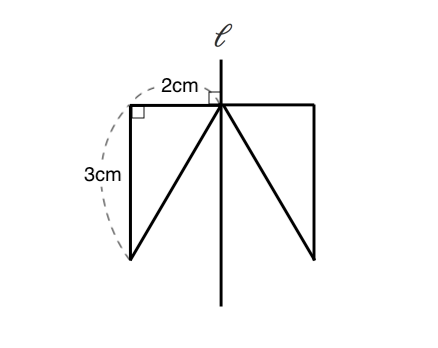



立体の体積を求める問題 回転させてできる立体 苦手な数学を簡単に




角柱 円柱の表面積と体積の公式 数学fun




多くの教師が失敗する角柱の体積の求め方 算数を究める
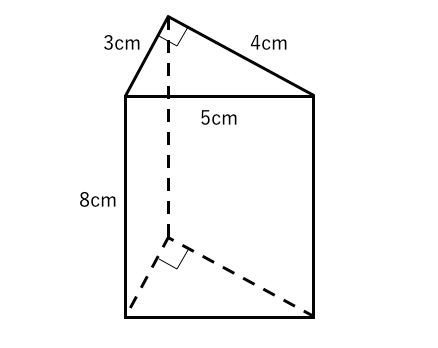



立体の表面積を求める 練習問題 苦手な数学を簡単に




体積の求め方 計算公式一覧




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




空間図形15 断頭三角柱の体積 Youtube




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



三角柱の体積の求め方 回転体の側面積の考え方 中学1年数学 空間図形




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題



展開図から三角錐の体積を求める 開智中学 先端a改題 09年 算数解法の極意




円錐の体積ってなんであの公式なの Webty Staff Blog




円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com



三角柱とは 体積 表面積の公式や求め方 計算問題 受験辞典



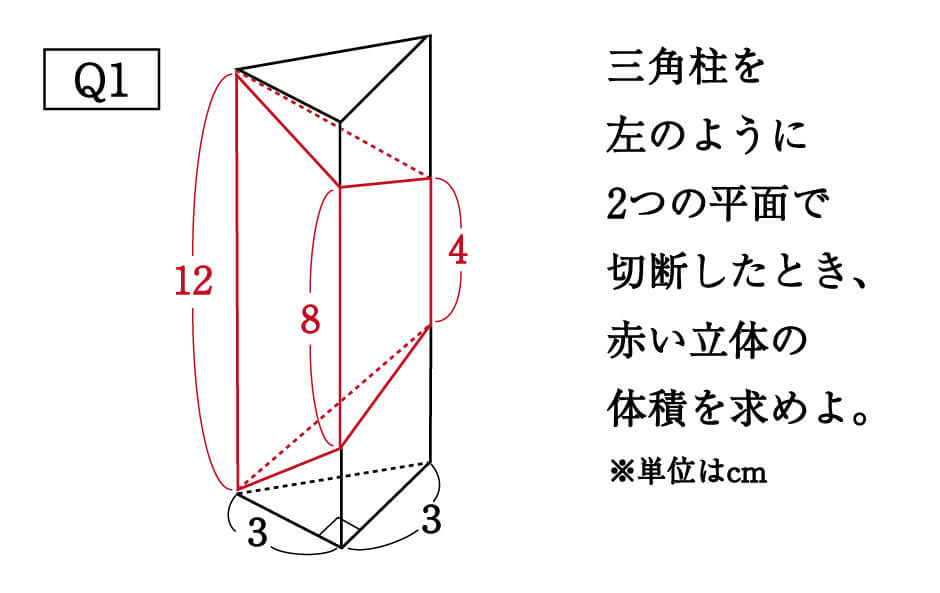
切断された三角柱 切断三角柱 の体積の求め方 まいにち一題 中学受験過去問題研究




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習




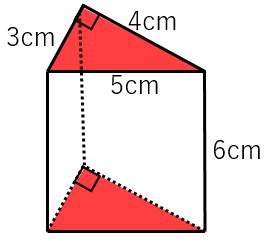
三角柱の投影図の体積の求め方を教えてください Clear




角錐 円錐の体積と表面積の公式 数学fun
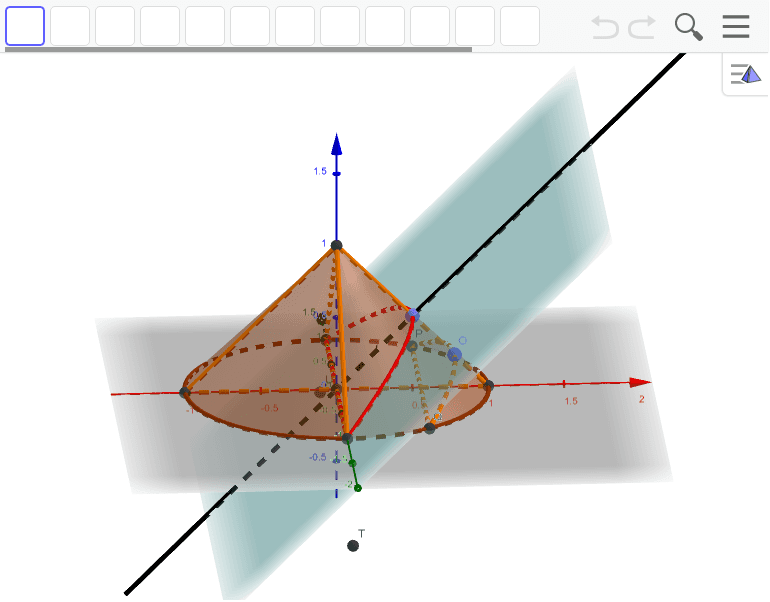



三角錐の体積の求め方 Geogebra




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ
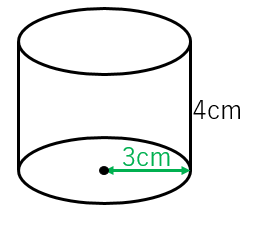



三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




角柱や円柱の表面積の求め方を教えてください Clear




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく



6年算数立体の体積その2 教え方




三角柱の表面積の求め方 問題を使って計算方法を解説するぞ 中学数学 理科の学習まとめサイト




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com



5 11 水の体積から三角柱の容器の高さを求めるには さんすうがく



三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




中学数学 三角柱の体積の求め方と公式 5秒でわかる なぜか分かる はかせちゃんの怪しい研究室




三角柱の体積の求め方 公式 小学生 中学生の勉強



小6 算数 小6 25 体積 円柱 角柱 Youtube




3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ




中3 三角形の相似 円錐の体積比 日本語版 Youtube




立体の体積を求める公式



小6 角柱と円柱の体積 三角柱の体積 日本語版 Youtube




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生



体積の計算 三角柱 製品設計知識



表面積や体積の求め方 三角柱 四角柱 円柱 球や半球




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




小5 複雑な立体の体積 直方体 日本語版 Youtube




6年算数立体の体積1 教え方




โน ตของ 体積 表面積 側面積 の公式 ช น Junior Clear




三角柱の体積の求め方 公式 小学生 中学生の勉強



数学 斜めに切断された三角柱の体積は こう解くべし 受験の秒殺テク 7 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ



三角柱の体積は 1分でわかる公式 計算 表面積の求め方



三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット
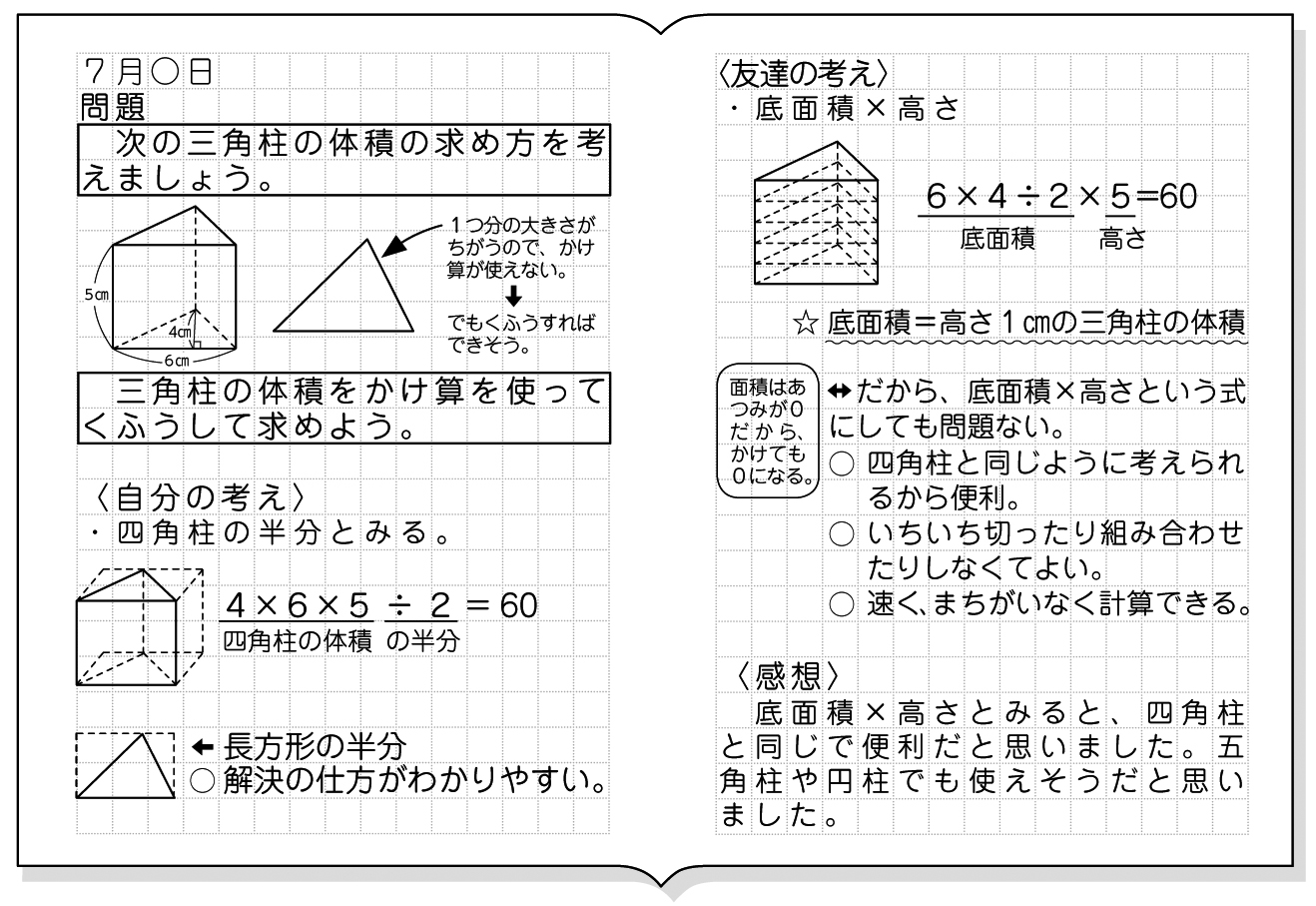



小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術



1




三角柱の体積の求め方 公式 小学生 中学生の勉強



1




公式を図解 すい体の体積 円すいの表面積の求め方




体積の求め方 計算公式一覧



6年算数立体の体積1 教え方




直感的に求めよう 直角三角形の面積の求め方 パパが教える算数教室




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




体積の求め方 計算公式一覧
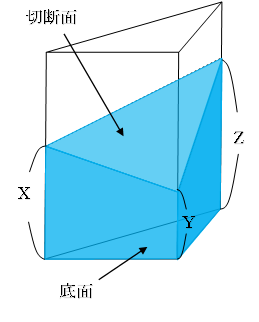



第9回 立体図形必勝法 角すいの切断 算数ドクター




三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学
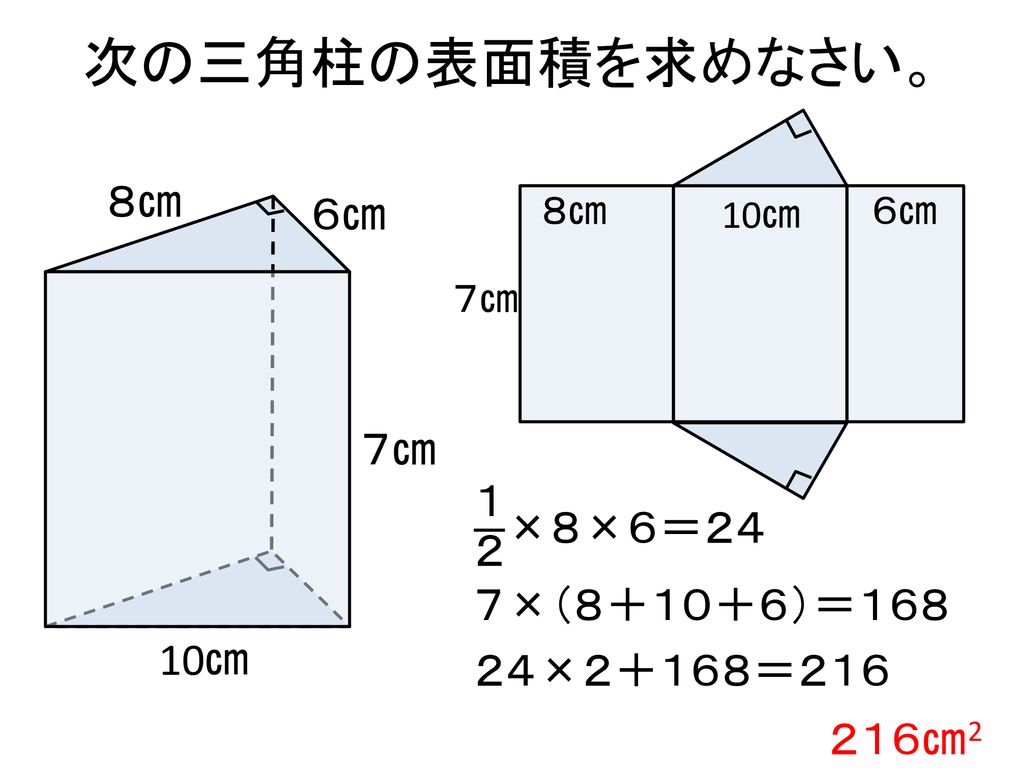



本時の目標 いろいろな立体の表面積を求めることができる Ppt Download




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス




多くの教師が失敗する角柱の体積の求め方 算数を究める




簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
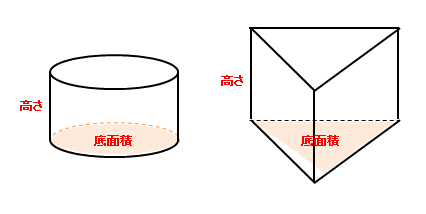



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー




計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




三角柱の体積の求め方 公式 小学生 中学生の勉強




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
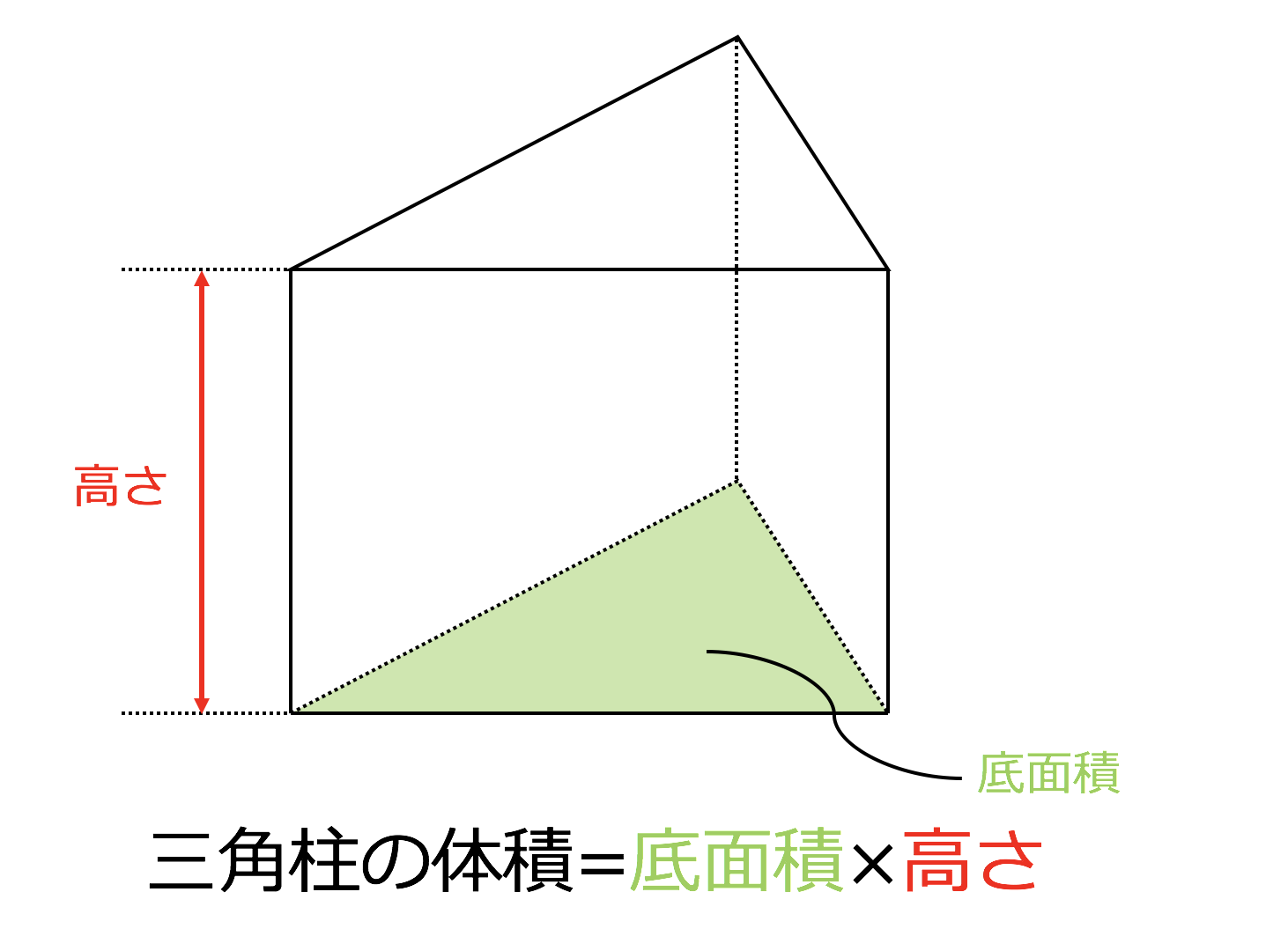



3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ




3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典
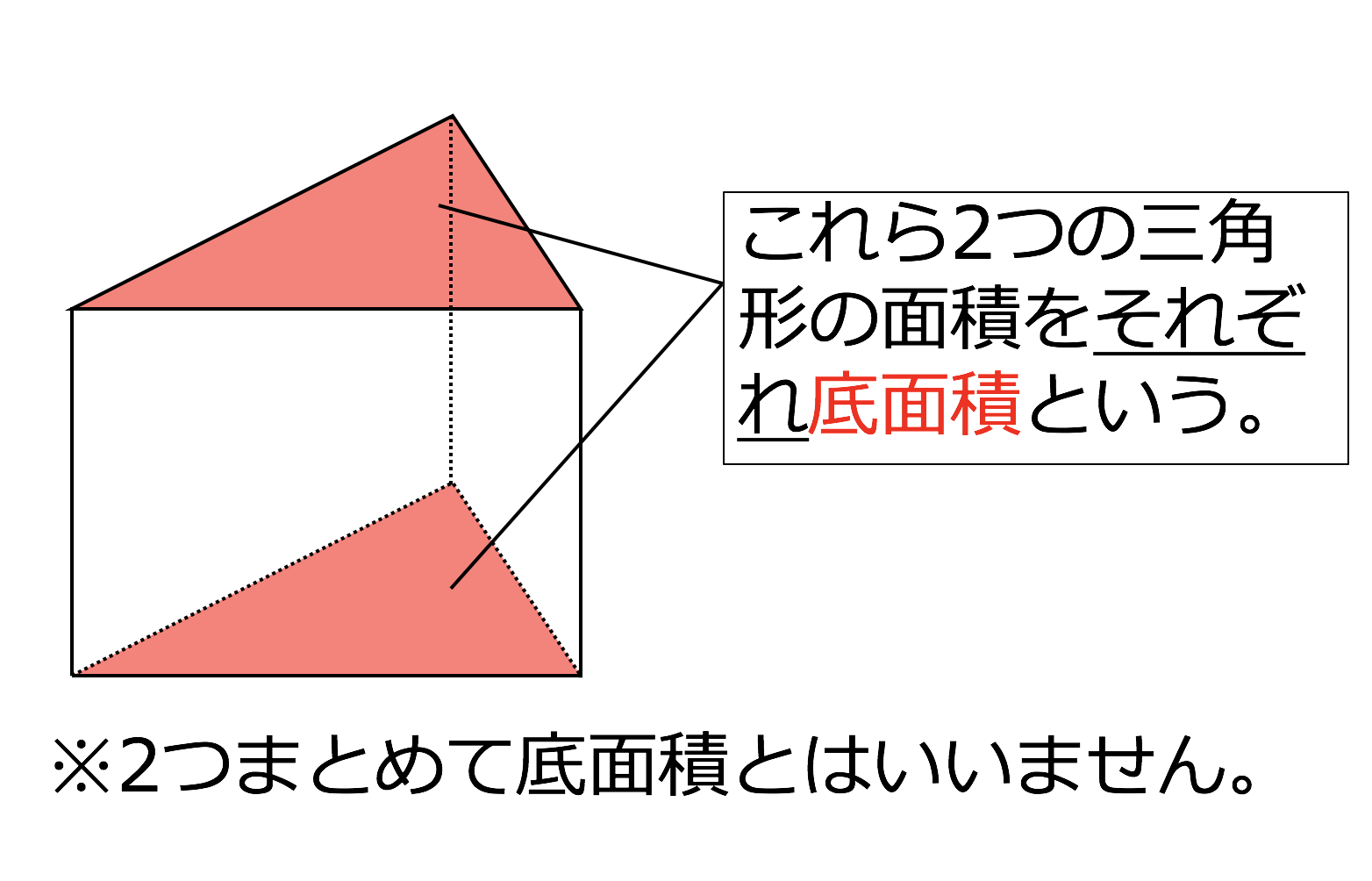



3分で分かる 三角柱の体積 表面積の公式 表面積 をわかりやすく 合格サプリ




体積 表面積




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿