感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
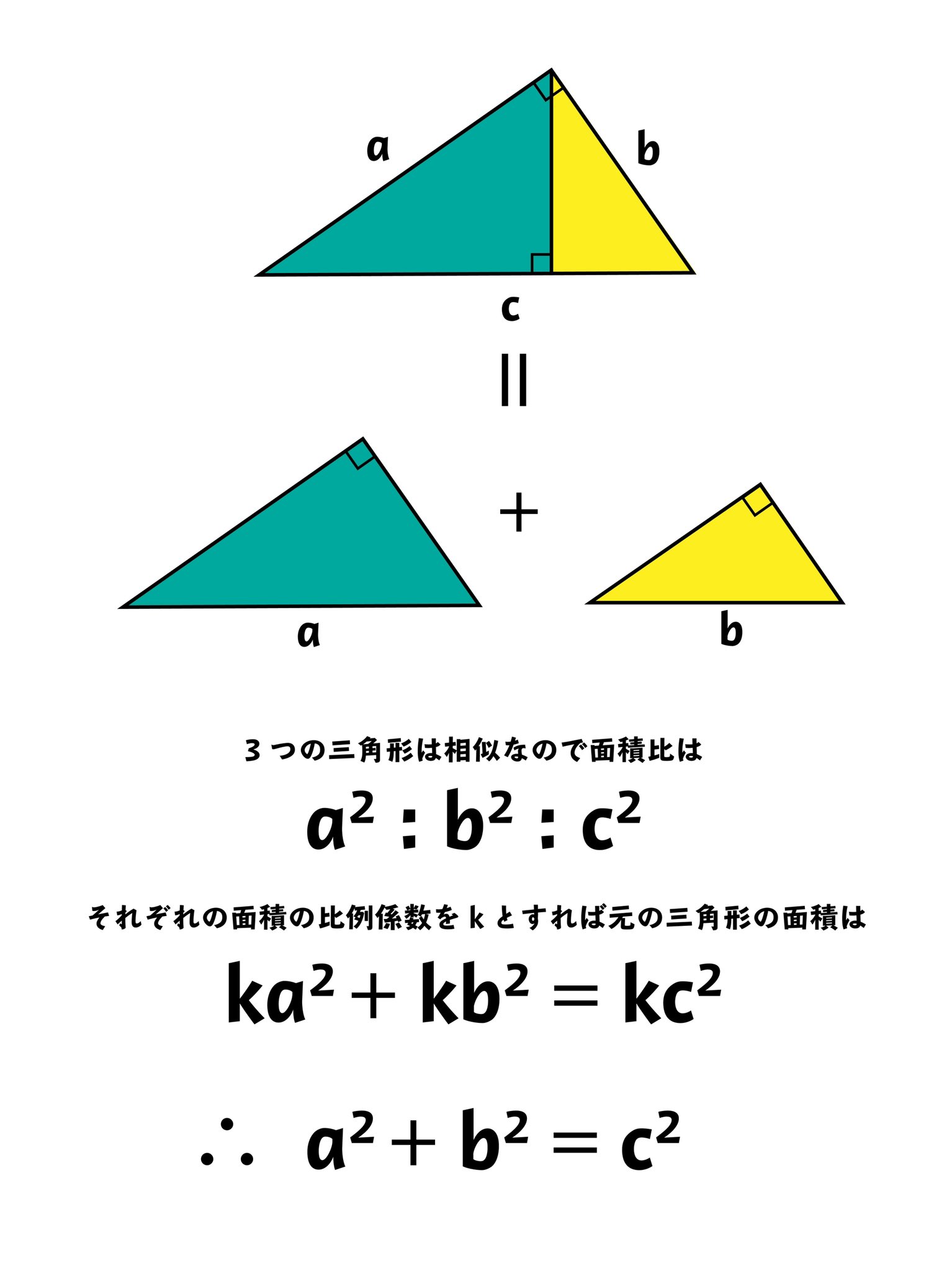
三平方の定理の証明⑭⑮～教科書に載っている証明方法をわかりやすく解説！ 実はインドのバスカラの証明だった？ ～ Fukusukeの数学めも この記事では、数ある三平方の定理の証明 3．三平方の定理の証明 さて、三平方の定理にもだいぶ慣れてきたと思います。 そこでこの定理を証明します。 公式は証明することで理解度がより増します。そのうえで暗記しましょ
三 平方 の 定理 の 証明
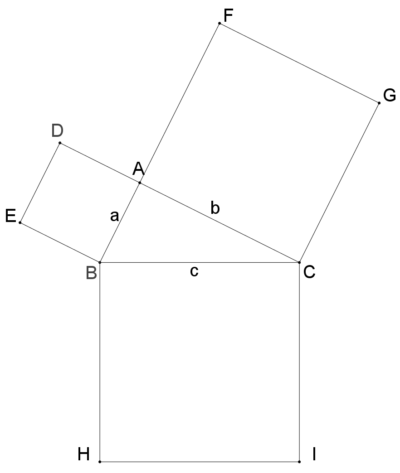
三 平方 の 定理 の 証明-三平方の定理の式 a2 b2 = c2 a 2 b 2 = c 2 より、 a2 = c2 −b2 a 2 = c 2 − b 2 ∴ a = √c2 −b2 ∴ a = c 2 − b 2 ① となるので、①式を使うと a a （底辺）の長さを求めることができます。 なので三平方の定理の証明と使い方 三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。 ここで、斜辺とは、直
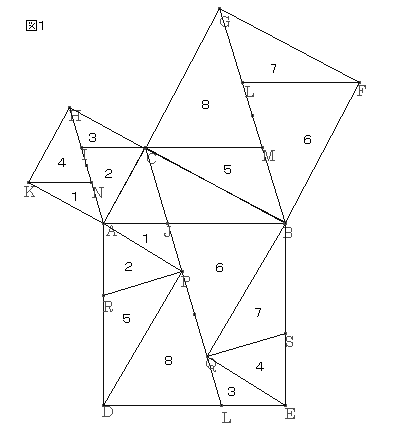
ピタゴラスの定理 の別証明集
は の 進付値で, の小数展開における 末 まつ 尾 び の番号を表し, 特に のときは〈割りきれる回数〉を表現するものでした 早速この定理を使って平方数の命題を始めたいと思います あ三平方の定理は「ピタゴラスの定理」とも呼ばれ、直角三角形の3辺の長さの関係を表す式のことである。 図のように直角三角形の斜辺をc, 他の2辺をa, bとすると c2 = a2 b2の関係が成り立つ。これを三平方の定理の逆といいます。 簡単にいうと 3つの辺を見比べて $$(一番長い辺)^2=(他の辺)^2(他の辺)^2$$ が成立するならば、その三角形は直角三角形になるぜ！ってことだね。 ちょっ
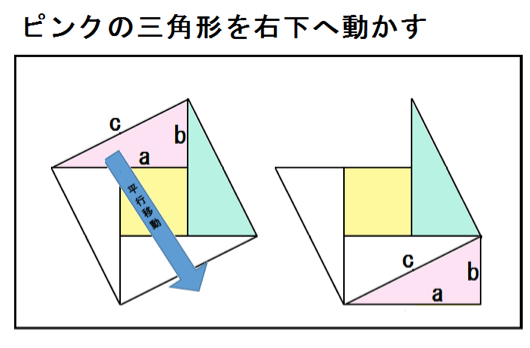
三平方の定理の証明 に Step4 右の四角形を等積変形 Step5 右の四角形を回転移動 Step6 右の四角形を等積変形 1．三平方の定理の証明その1 まずは良く知られた、最もポピュラー（？ ）な証明方法をご紹介します。 まず、直角三角形ABCを準備します。 長さが と （ とします）、斜辺を とし三角形の角の反対側にある辺を対辺と言います。 そして 特に直角の対辺を斜辺を言います。 また、当然ですが、三角なので辺は3つあります。 三平方の定理とは、 『斜辺の2乗が、その他の辺の2乗
三 平方 の 定理 の 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
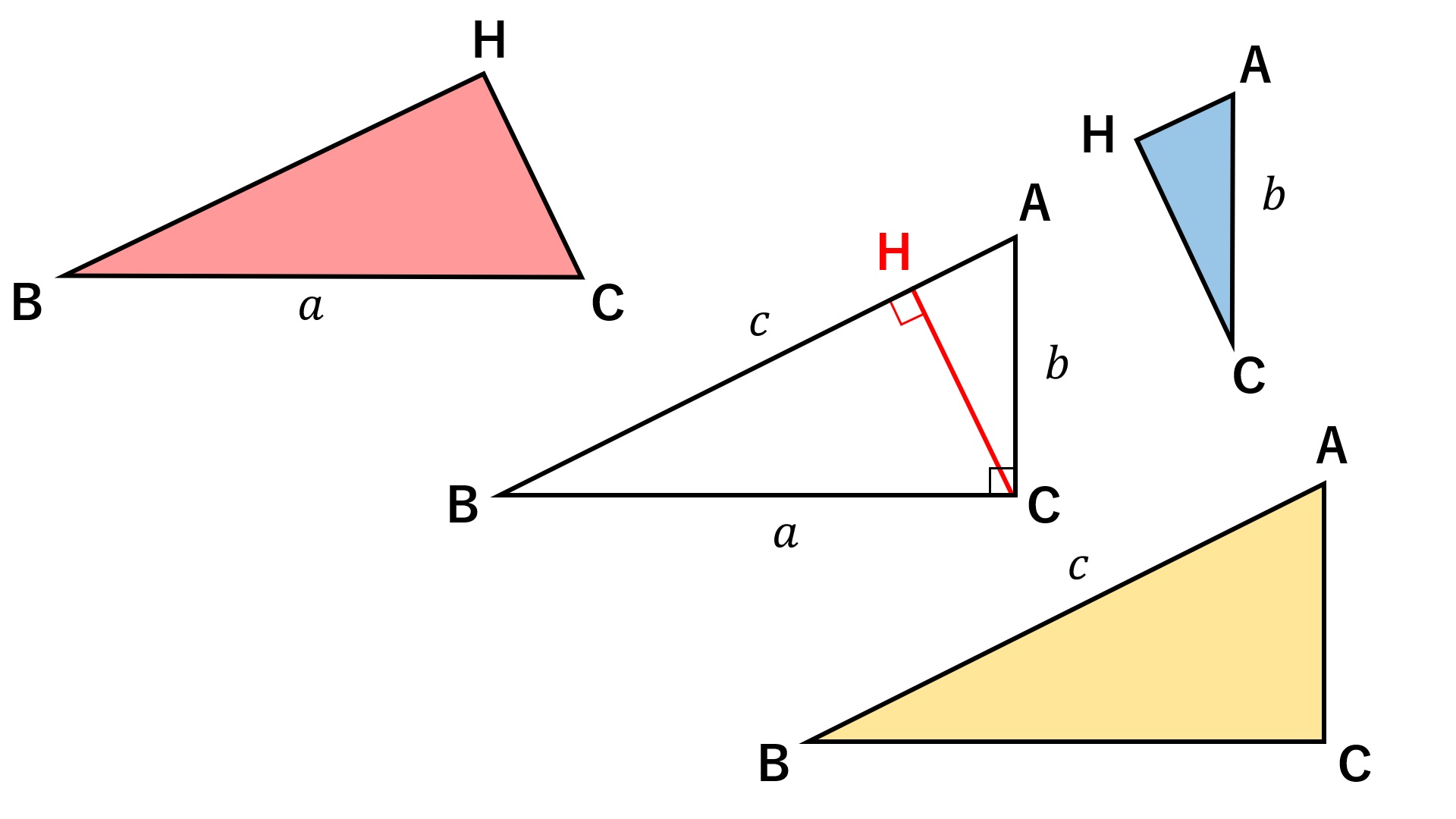 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 | 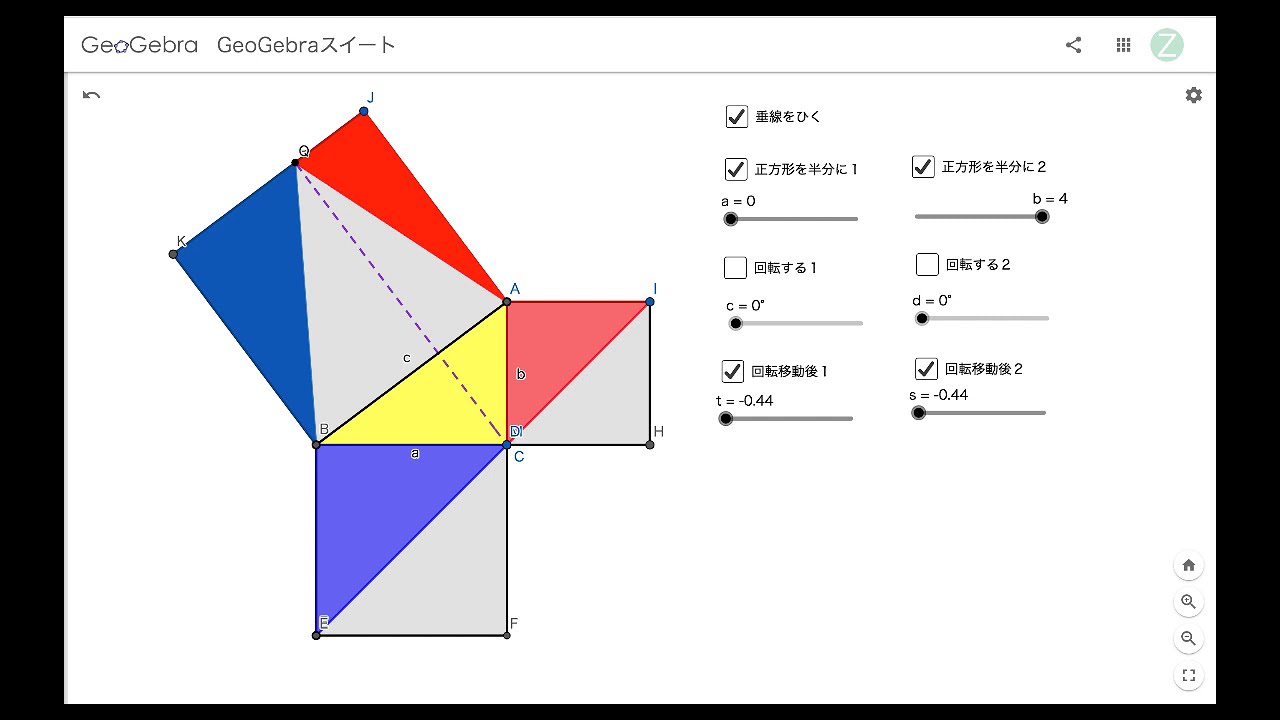 三平方の定理の証明と使い方 |
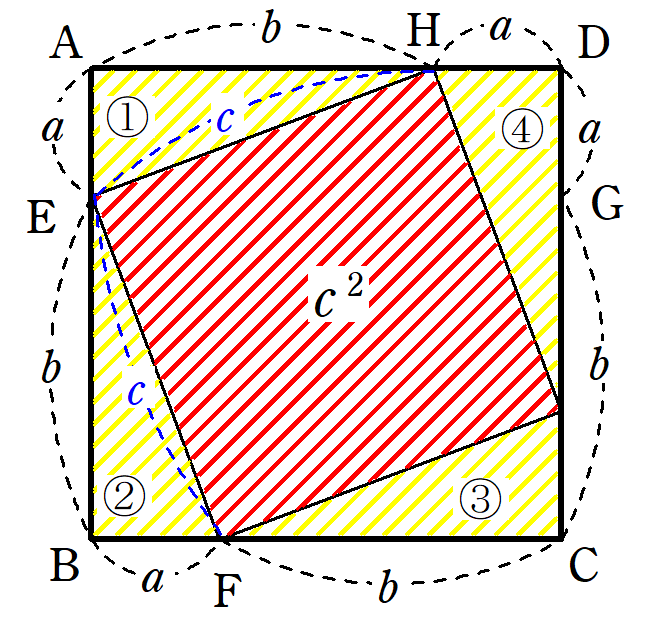 三平方の定理の証明と使い方 | 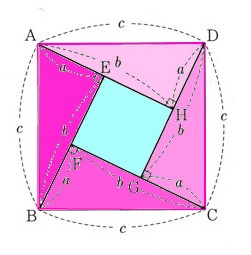 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
三平方の定理の証明と使い方 | 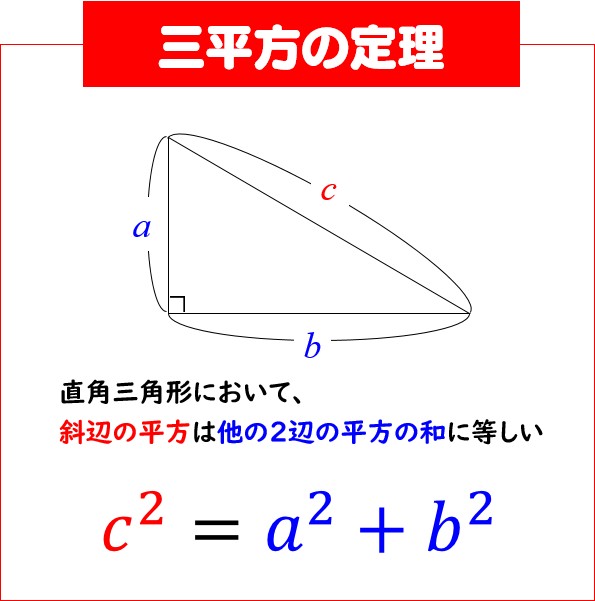 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
「三 平方 の 定理 の 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方の定理の証明と使い方 | 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
「三 平方 の 定理 の 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 | 三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 | 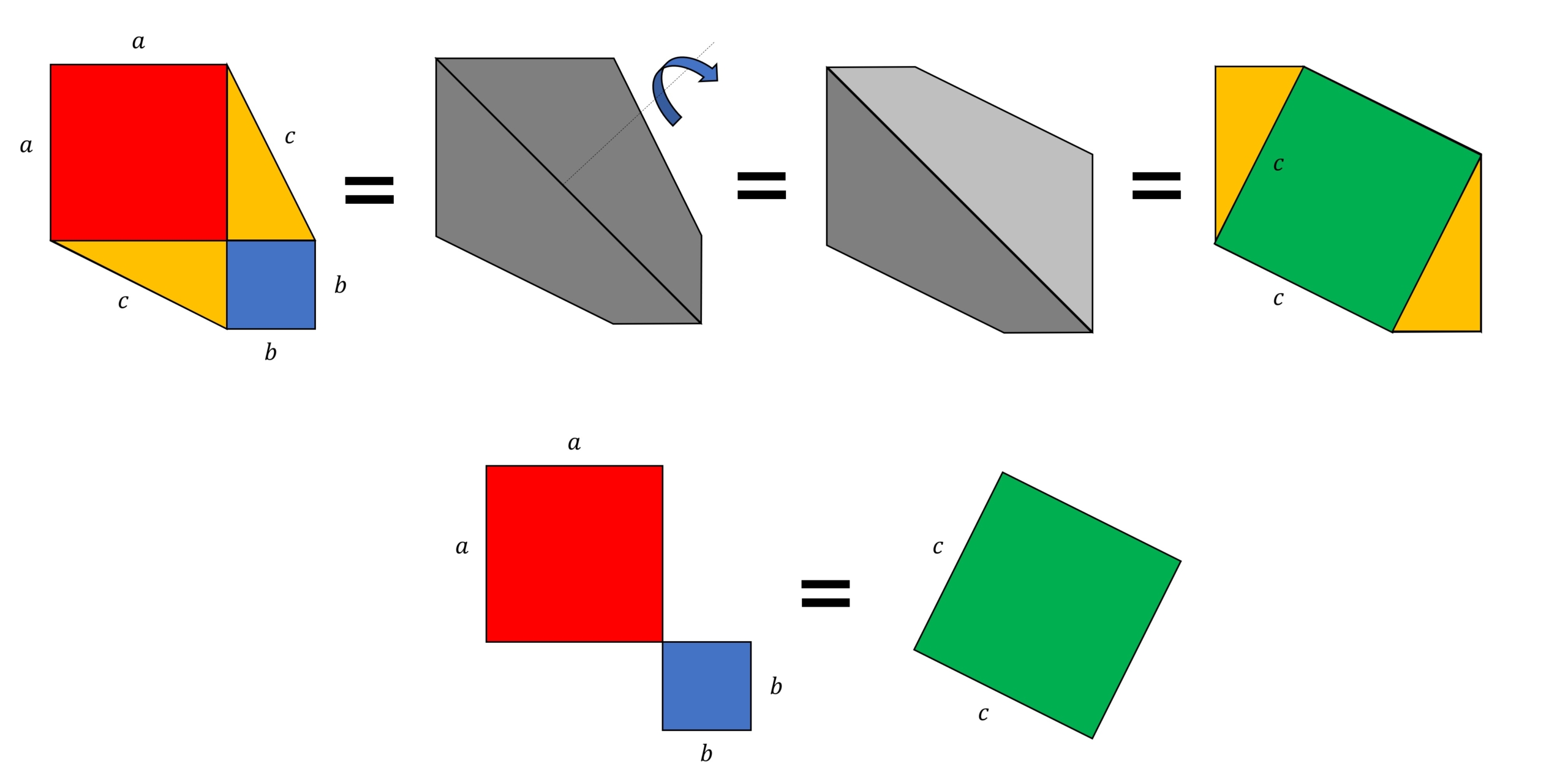 三平方の定理の証明と使い方 | 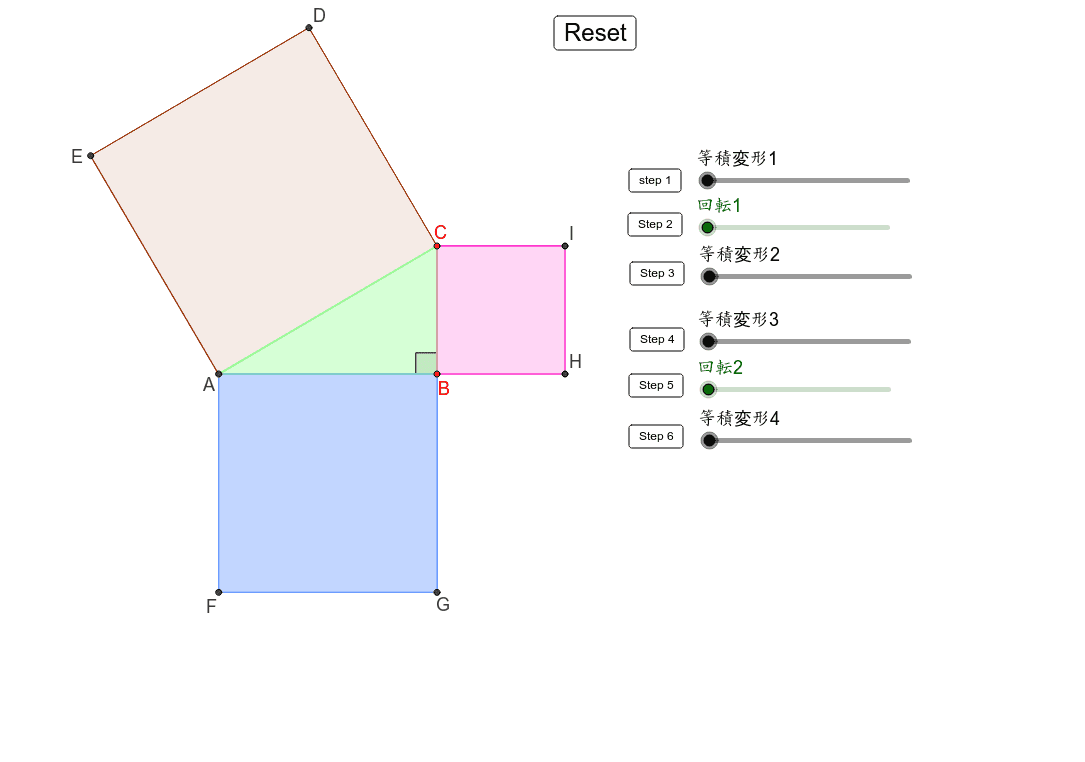 三平方の定理の証明と使い方 |
「三 平方 の 定理 の 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 | 三平方の定理の証明と使い方 | 三平方の定理の証明と使い方 |
「三 平方 の 定理 の 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方の定理の証明と使い方 | 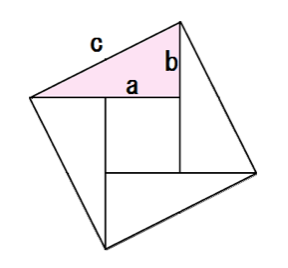 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 | 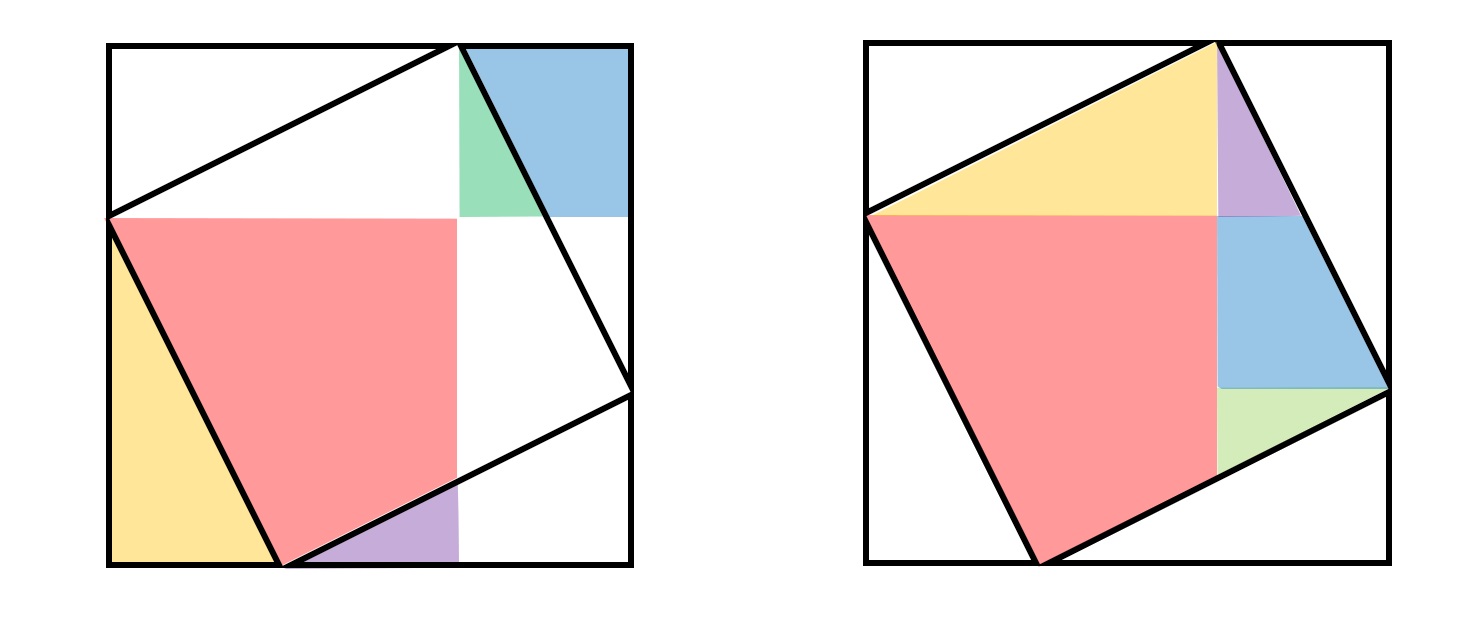 三平方の定理の証明と使い方 | 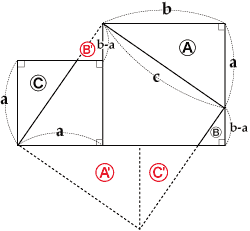 三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 | 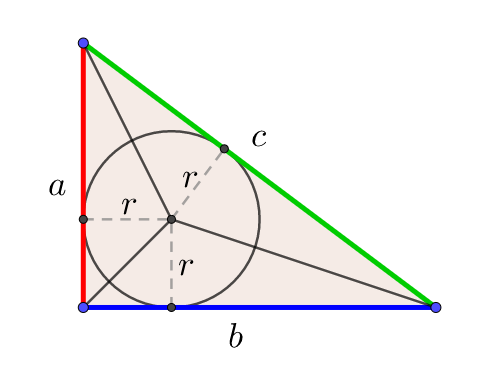 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
「三 平方 の 定理 の 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
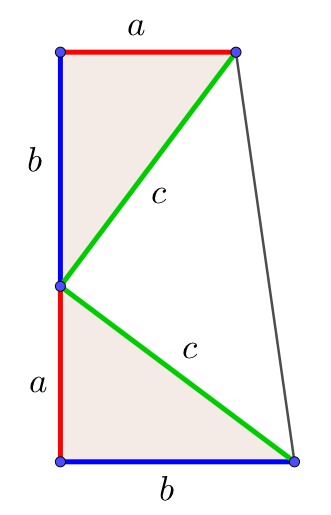 三平方の定理の証明と使い方 | 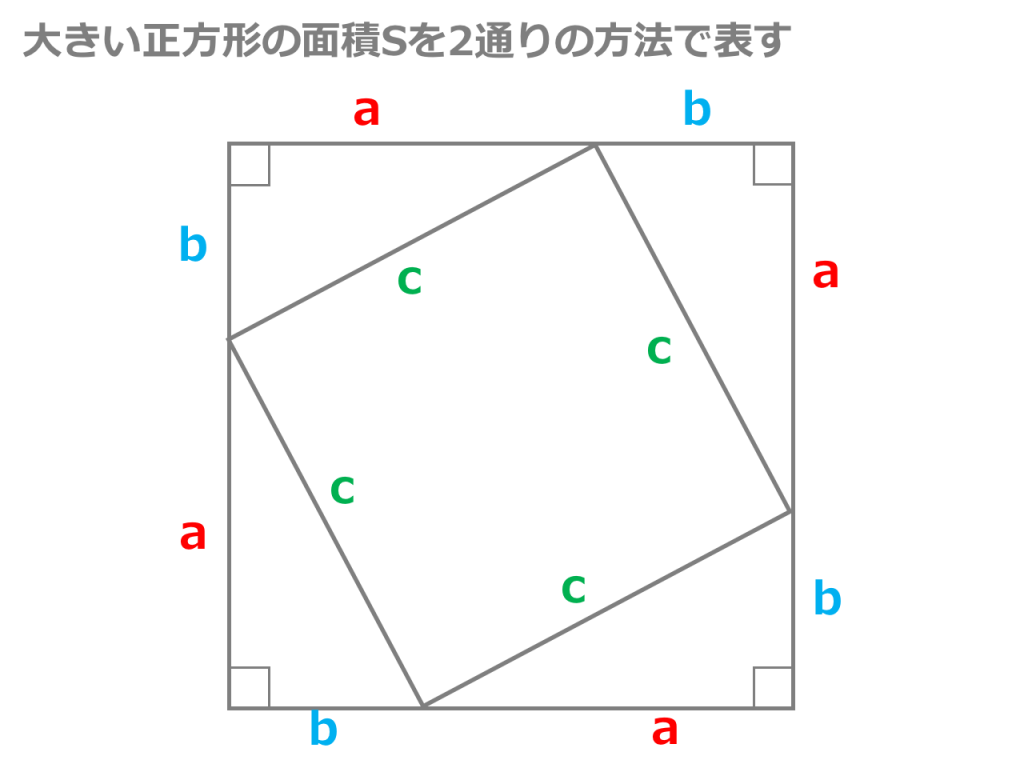 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 | 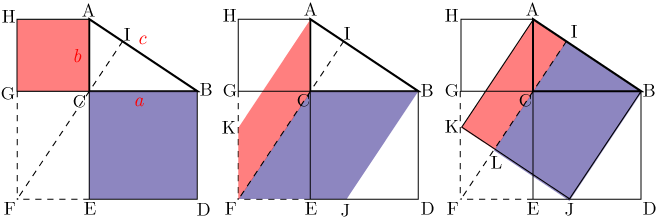 三平方の定理の証明と使い方 | 三平方の定理の証明と使い方 |
三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
「三 平方 の 定理 の 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |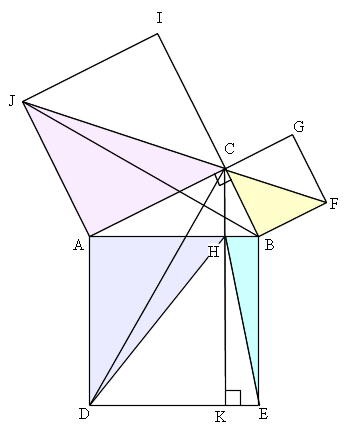
三平方の定理の証明と使い方 |  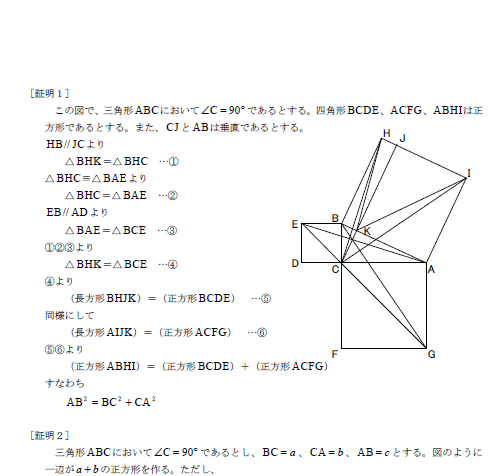三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
「三 平方 の 定理 の 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
「三 平方 の 定理 の 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 | 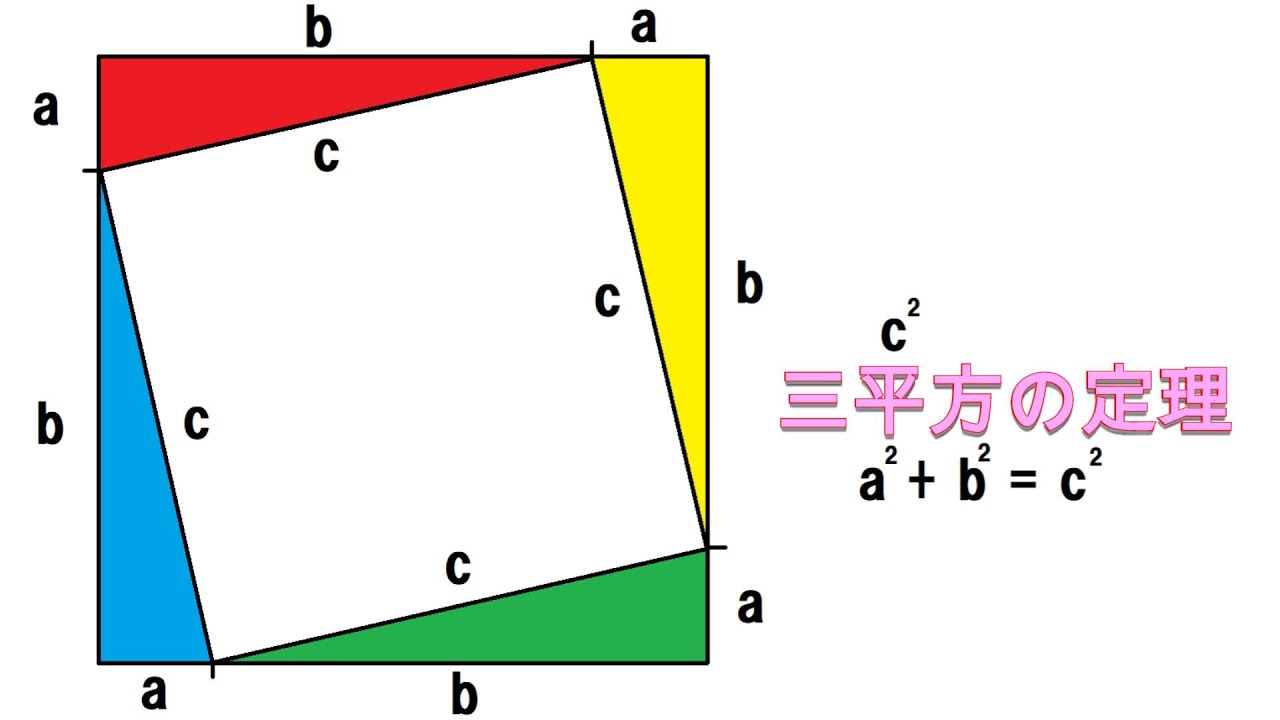 三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 | 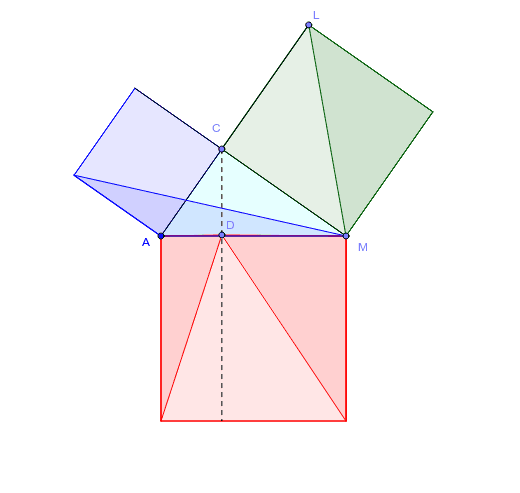 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 | 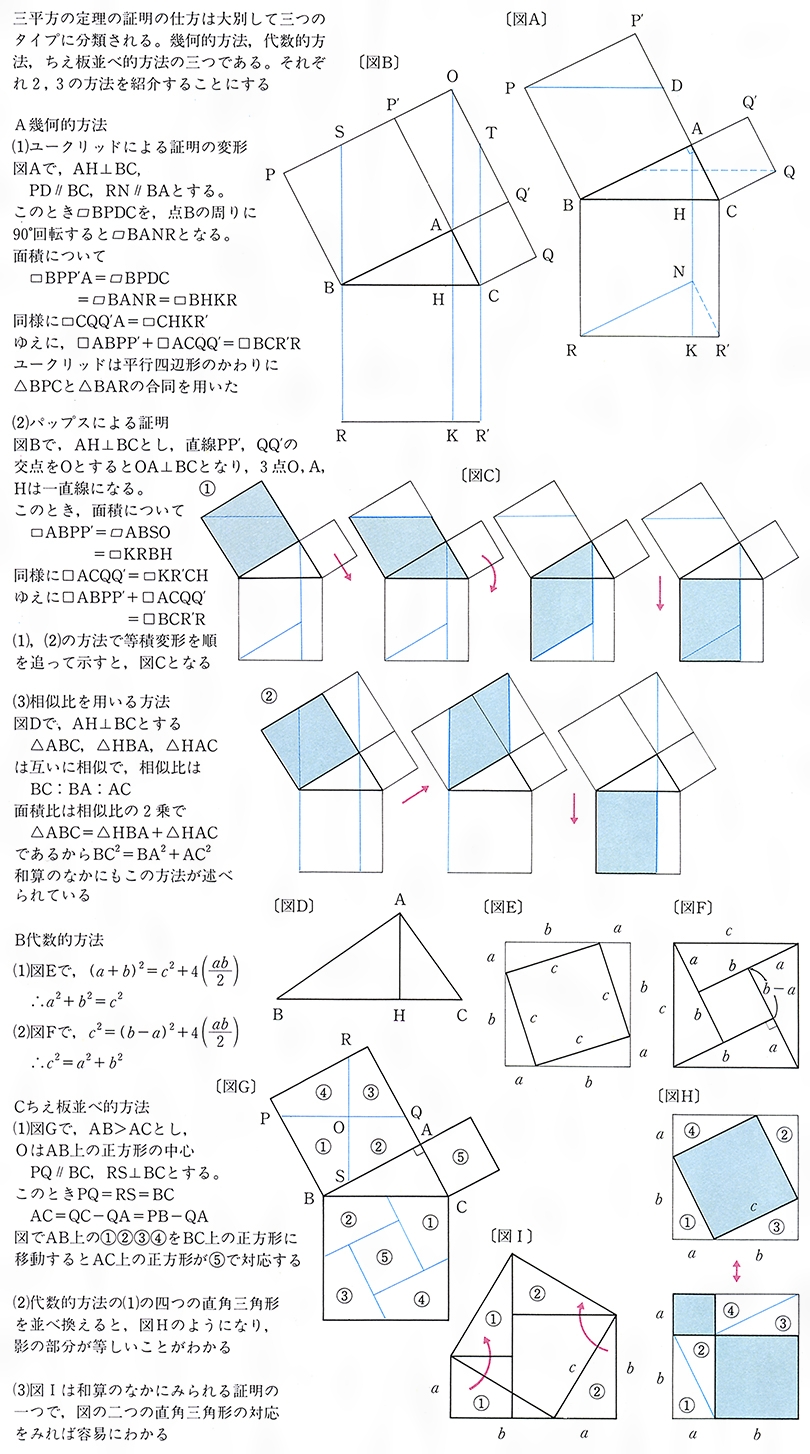 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
「三 平方 の 定理 の 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方の定理の証明と使い方 | 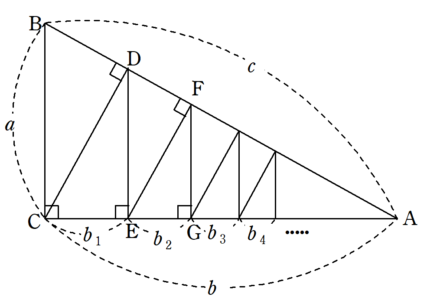 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 | 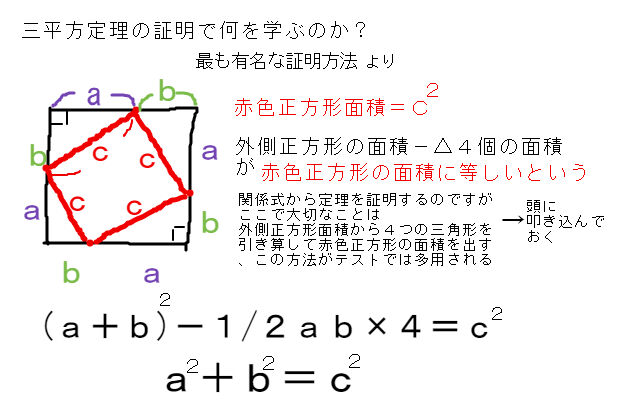 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
「三 平方 の 定理 の 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 | 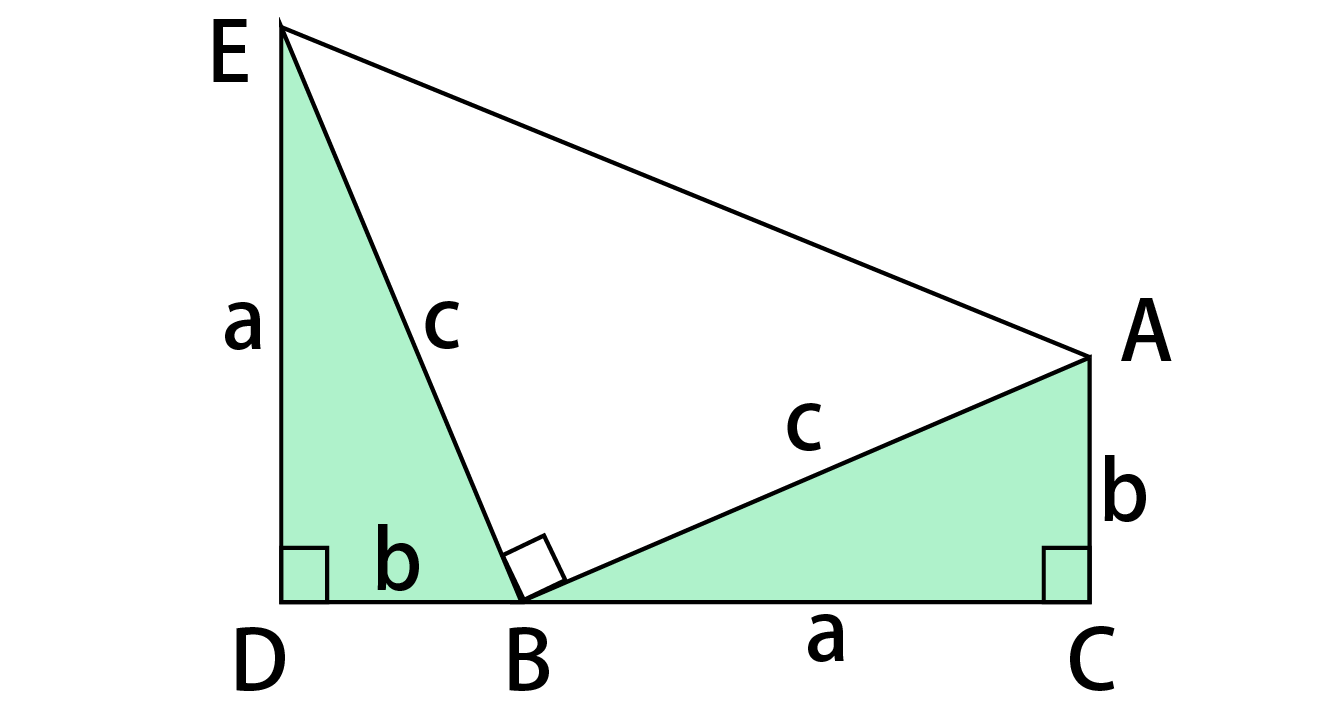 三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
「三 平方 の 定理 の 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |  三平方の定理の証明と使い方 |
 三平方の定理の証明と使い方 | 三平方の定理の証明と使い方 |
三平方の定理のチェックリスト 21年12月3日 21年12月7日 dora 三平方の定理とは何か知っているか 三平方の定理を証明することができるか 三平方の定理を利用して, 直角三角形 ①＝②の等式を解くと，三平方の定理の証明が完了します。 \begin{align} ①& =②\\ a^22abb^2 & = 2abc^2\\ a^2b^2& = c^2 \\ \end{align} 正方形と直角三角形を使った証明② 教
0 件のコメント:
コメントを投稿